Related Research Articles
In computability theory, the Church–Turing thesis is a hypothesis about the nature of computable functions. It states that a function on the natural numbers can be calculated by an effective method if and only if it is computable by a Turing machine. The thesis is named after American mathematician Alonzo Church and the British mathematician Alan Turing. Before the precise definition of computable function, mathematicians often used the informal term effectively calculable to describe functions that are computable by paper-and-pencil methods. In the 1930s, several independent attempts were made to formalize the notion of computability:
Computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.

In computability theory and computational complexity theory, a decision problem is a problem that can be posed as a yes–no question of the input values. An example of a decision problem is deciding whether a given natural number is prime. Another is the problem "given two numbers x and y, does x evenly divide y?". The answer is either 'yes' or 'no' depending upon the values of x and y. A method for solving a decision problem, given in the form of an algorithm, is called a decision procedure for that problem. A decision procedure for the decision problem "given two numbers x and y, does x evenly divide y?" would give the steps for determining whether x evenly divides y. One such algorithm is long division. If the remainder is zero the answer is 'yes', otherwise it is 'no'. A decision problem which can be solved by an algorithm is called decidable.
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to solve certain decision problems in a single operation. The problem can be of any complexity class. Even undecidable problems, such as the halting problem, can be used.
In computability theory, Rice's theorem states that all non-trivial, semantic properties of programs are undecidable. A semantic property is one about the program's behavior, unlike a syntactic property. A property is non-trivial if it is neither true for every partial computable function, nor false for every partial computable function.

In theoretical computer science and mathematics, the theory of computation is the branch that deals with what problems can be solved on a model of computation, using an algorithm, how efficiently they can be solved or to what degree. The field is divided into three major branches: automata theory and formal languages, computability theory, and computational complexity theory, which are linked by the question: "What are the fundamental capabilities and limitations of computers?".
In mathematics, logic and computer science, a formal language is called recursively enumerable if it is a recursively enumerable subset in the set of all possible words over the alphabet of the language, i.e., if there exists a Turing machine which will enumerate all valid strings of the language.
Computability theory, also known as recursion theory, is a branch of mathematical logic, computer science, and the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since expanded to include the study of generalized computability and definability. In these areas, computability theory overlaps with proof theory and effective descriptive set theory.
In computability theory, a set S of natural numbers is called computably enumerable (c.e.), recursively enumerable (r.e.), semidecidable, partially decidable, listable, provable or Turing-recognizable if:
In computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Thus reductions can be used to measure the relative computational difficulty of two problems. It is said that A reduces to B if, in layman's terms, B is harder to solve than A. That is to say, any algorithm that solves B can also be used as part of a program that solves A.
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science. The computability of a problem is closely linked to the existence of an algorithm to solve the problem.

In computational complexity theory, a complexity class is a set of computational problems of related resource-based complexity. The two most commonly analyzed resources are time and memory.
In computational complexity theory, P, also known as PTIME or DTIME(nO ), is a fundamental complexity class. It contains all decision problems that can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.
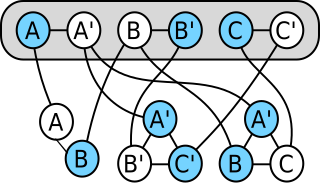
In computability theory and computational complexity theory, a reduction is an algorithm for transforming one problem into another problem. A sufficiently efficient reduction from one problem to another may be used to show that the second problem is at least as difficult as the first.
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithms, in the sense that a function is computable if there exists an algorithm that can do the job of the function, i.e. given an input of the function domain it can return the corresponding output. Computable functions are used to discuss computability without referring to any concrete model of computation such as Turing machines or register machines. Any definition, however, must make reference to some specific model of computation but all valid definitions yield the same class of functions. Particular models of computability that give rise to the set of computable functions are the Turing-computable functions and the general recursive functions.
In computability theory, a Turing reduction from a decision problem to a decision problem is an oracle machine which decides problem given an oracle for . It can be understood as an algorithm that could be used to solve if it had available to it a subroutine for solving B. The concept can be analogously applied to function problems.
In computability theory, a machine that always halts, also called a decider or a total Turing machine, is a Turing machine that eventually halts for every input.
In computability theory and computational complexity theory, RE is the class of decision problems for which a 'yes' answer can be verified by a Turing machine in a finite amount of time. Informally, it means that if the answer to a problem instance is 'yes', then there is some procedure that takes finite time to determine this, and this procedure never falsely reports 'yes' when the true answer is 'no'. However, when the true answer is 'no', the procedure is not required to halt; it may go into an "infinite loop" for some 'no' cases. Such a procedure is sometimes called a semi-algorithm, to distinguish it from an algorithm, defined as a complete solution to a decision problem.
PR is the complexity class of all primitive recursive functions—or, equivalently, the set of all formal languages that can be decided in time bounded by such a function. This includes addition, multiplication, exponentiation, tetration, etc.
In computational complexity theory, a certificate is a string that certifies the answer to a computation, or certifies the membership of some string in a language. A certificate is often thought of as a solution path within a verification process, which is used to check whether a problem gives the answer "Yes" or "No".
References
- Blum, Lenore, Mike Shub, and Steve Smale, (1989), "On a theory of computation and complexity over the real numbers: NP-completeness, recursive functions and universal machines", Bulletin of the American Mathematical Society , New Series, 21 (1): 1-46.