Co-NP

Last updated
Unsolved problem in computer science:
⁠⁠
(more unsolved problems in computer science)

In computational complexity theory, co-NP is a complexity class. A decision problem X is a member of co-NP if and only if its complement X is in the complexity class NP. The class can be defined as follows: a decision problem is in co-NP if and only if for every no-instance we have a polynomial-length "certificate" and there is a polynomial-time algorithm that can be used to verify any purported certificate.

Contents

That is, co-NP is the set of decision problems where there exists a polynomial ⁠⁠ and a polynomial-time bounded Turing machine M such that for every instance x, x is a no-instance if and only if: for some possible certificate c of length bounded by ⁠⁠, the Turing machine M accepts the pair (x, c). [1]

Complementary problems

While an NP problem asks whether a given instance is a yes-instance, its complement asks whether an instance is a no-instance, which means the complement is in co-NP. Any yes-instance for the original NP problem becomes a no-instance for its complement, and vice versa.

Unsatisfiability

An example of an NP-complete problem is the Boolean satisfiability problem: given a Boolean formula, is it satisfiable (is there a possible input for which the formula outputs true)? The complementary problem asks: "given a Boolean formula, is it unsatisfiable (do all possible inputs to the formula output false)?". Since this is the complement of the satisfiability problem, a certificate for a no-instance is the same as for a yes-instance from the original NP problem: a set of Boolean variable assignments which make the formula true. On the other hand, a certificate of a yes-instance for the complementary problem (whatever form it might take) would be equally as complex as for the no-instance of the original NP satisfiability problem.

co-NP-completeness

A problem L is co-NP-complete if and only if L is in co-NP and for any problem in co-NP, there exists a polynomial-time reduction from that problem to L.

Tautology reduction

Determining if a formula in propositional logic is a tautology is co-NP-complete: that is, if the formula evaluates to true under every possible assignment to its variables. [1]

Relationship to other classes

Inclusions of complexity classes including P, NP, co-NP, BPP, P/poly, PH, and PSPACE Complexity-classes-polynomial.svg
Inclusions of complexity classes including P, NP, co-NP, BPP, P/poly, PH, and PSPACE

P, the class of polynomial time solvable problems, is a subset of both NP and co-NP. P is thought to be a strict subset in both cases. Because P is closed under complementation, and NP and co-NP are complementary, it cannot be strict in one case and not strict in the other: if P equals NP, it must also equal co-NP, and vice versa. [2]

NP and co-NP are also thought to be unequal. [3] If so, then no NP-complete problem can be in co-NP and no co-NP-complete problem can be in NP. [4] This can be shown as follows. Suppose for the sake of contradiction there exists an NP-complete problem X that is in co-NP. Since all problems in NP can be reduced to X, it follows that for every problem in NP, we can construct a non-deterministic Turing machine that decides its complement in polynomial time; i.e., ⁠⁠. From this, it follows that the set of complements of the problems in NP is a subset of the set of complements of the problems in co-NP; i.e., ⁠⁠. Thus ⁠⁠. The proof that no co-NP-complete problem can be in NP if ⁠⁠ is symmetrical.

co-NP is a subset of PH, which itself is a subset of PSPACE.

Integer factorization

An example of a problem that is known to belong to both NP and co-NP (but not known to be in P) is Integer factorization: given positive integers m and n, determine if m has a factor less than n and greater than one. Membership in NP is clear; if m does have such a factor, then the factor itself is a certificate. Membership in co-NP is also straightforward: one can just list the prime factors of m, all greater or equal to n, which the verifier can confirm to be valid by multiplication and the AKS primality test. It is presently not known whether there is a polynomial-time algorithm for factorization, equivalently that integer factorization is in P, and hence this example is interesting as one of the most natural problems known to be in NP and co-NP but not known to be in P. [5]

Related Research Articles

In computational complexity theory, a branch of computer science, bounded-error probabilistic polynomial time (BPP) is the class of decision problems solvable by a probabilistic Turing machine in polynomial time with an error probability bounded by 1/3 for all instances. BPP is one of the largest practical classes of problems, meaning most problems of interest in BPP have efficient probabilistic algorithms that can be run quickly on real modern machines. BPP also contains P, the class of problems solvable in polynomial time with a deterministic machine, since a deterministic machine is a special case of a probabilistic machine.

The P versus NP problem is a major unsolved problem in theoretical computer science. Informally, it asks whether every problem whose solution can be quickly verified can also be quickly solved.

In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and explores the relationships between these classifications. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.

<span class="mw-page-title-main">NP (complexity)</span> Complexity class used to classify decision problems

In computational complexity theory, NP is a complexity class used to classify decision problems. NP is the set of decision problems for which the problem instances, where the answer is "yes", have proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively the set of problems that can be solved in polynomial time by a nondeterministic Turing machine.

In computational complexity theory, the complexity class #P (pronounced "sharp P" or, sometimes "number P" or "hash P") is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute f(x)", where f is the number of accepting paths of a nondeterministic Turing machine running in polynomial time. Unlike most well-known complexity classes, it is not a class of decision problems but a class of function problems. The most difficult, representative problems of this class are #P-complete.

In complexity theory, computational problems that are co-NP-complete are those that are the hardest problems in co-NP, in the sense that any problem in co-NP can be reformulated as a special case of any co-NP-complete problem with only polynomial overhead. If P is different from co-NP, then all of the co-NP-complete problems are not solvable in polynomial time. If there exists a way to solve a co-NP-complete problem quickly, then that algorithm can be used to solve all co-NP problems quickly.

<span class="mw-page-title-main">NP-hardness</span> Complexity class

In computational complexity theory, a computational problem H is called NP-hard if, for every problem L which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from L to H. That is, assuming a solution for H takes 1 unit time, H's solution can be used to solve L in polynomial time. As a consequence, finding a polynomial time algorithm to solve a single NP-hard problem would give polynomial time algorithms for all the problems in the complexity class NP. As it is suspected, but unproven, that P≠NP, it is unlikely that any polynomial-time algorithms for NP-hard problems exist.

In computational complexity theory, randomized polynomial time (RP) is the complexity class of problems for which a probabilistic Turing machine exists with these properties:

In complexity theory, UP is the complexity class of decision problems solvable in polynomial time on an unambiguous Turing machine with at most one accepting path for each input. UP contains P and is contained in NP.

<span class="mw-page-title-main">Complexity class</span> Set of problems in computational complexity theory

In computational complexity theory, a complexity class is a set of computational problems "of related resource-based complexity". The two most commonly analyzed resources are time and memory.

In computer science, parameterized complexity is a branch of computational complexity theory that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input or output. The complexity of a problem is then measured as a function of those parameters. This allows the classification of NP-hard problems on a finer scale than in the classical setting, where the complexity of a problem is only measured as a function of the number of bits in the input. This appears to have been first demonstrated in Gurevich, Stockmeyer & Vishkin (1984). The first systematic work on parameterized complexity was done by Downey & Fellows (1999).

In computational complexity theory, P, also known as PTIME or DTIME(nO(1)), is a fundamental complexity class. It contains all decision problems that can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.

In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes NP and co-NP. Each class in the hierarchy is contained within PSPACE. The hierarchy can be defined using oracle machines or alternating Turing machines. It is a resource-bounded counterpart to the arithmetical hierarchy and analytical hierarchy from mathematical logic. The union of the classes in the hierarchy is denoted PH.

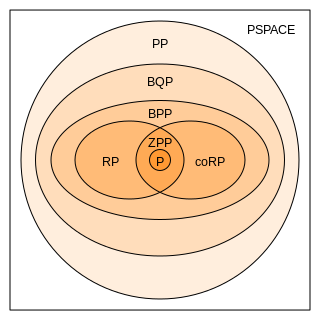
<span class="mw-page-title-main">PP (complexity)</span> Class of problems in computer science

In complexity theory, PP, or PPT is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time. The complexity class was defined by Gill in 1977.

In computational complexity theory, the Cook–Levin theorem, also known as Cook's theorem, states that the Boolean satisfiability problem is NP-complete. That is, it is in NP, and any problem in NP can be reduced in polynomial time by a deterministic Turing machine to the Boolean satisfiability problem.

In computational complexity theory, a function problem is a computational problem where a single output is expected for every input, but the output is more complex than that of a decision problem. For function problems, the output is not simply 'yes' or 'no'.

In computational complexity theory, the class APX is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant. In simple terms, problems in this class have efficient algorithms that can find an answer within some fixed multiplicative factor of the optimal answer.

In computational complexity theory, the language TQBF is a formal language consisting of the true quantified Boolean formulas. A (fully) quantified Boolean formula is a formula in quantified propositional logic where every variable is quantified, using either existential or universal quantifiers, at the beginning of the sentence. Such a formula is equivalent to either true or false. If such a formula evaluates to true, then that formula is in the language TQBF. It is also known as QSAT.

<span class="mw-page-title-main">NP-completeness</span> Complexity class

In computational complexity theory, a problem is NP-complete when:

  1. It is a decision problem, meaning that for any input to the problem, the output is either "yes" or "no".
  2. When the answer is "yes", this can be demonstrated through the existence of a short solution.
  3. The correctness of each solution can be verified quickly and a brute-force search algorithm can find a solution by trying all possible solutions.
  4. The problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. In this sense, NP-complete problems are the hardest of the problems to which solutions can be verified quickly. If we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified.

In computational complexity theory, NP/poly is a complexity class, a non-uniform analogue of the class NP of problems solvable in polynomial time by a non-deterministic Turing machine. It is the non-deterministic complexity class corresponding to the deterministic class P/poly.

References

  1. 1 2 Arora, Sanjeev; Barak, Boaz (2009). Complexity Theory: A Modern Approach. Cambridge University Press. p. 56. ISBN   978-0-521-42426-4.
  2. ↑ Mayordomo, Elvira (2004). "P versus NP". Monografías de la Real Academia de Ciencias de Zaragoza. 26: 57–68.
  3. ↑ Hopcroft, John E. (2000). Introduction to Automata Theory, Languages, and Computation (2nd ed.). Boston: Addison-Wesley. ISBN   0-201-44124-1. Chap. 11.
  4. ↑ Goldreich, Oded (2010). P, NP, and NP-completeness: The Basics of Computational Complexity. Cambridge University Press. p. 155. ISBN   9781139490092.
  5. ↑ Aaronson, Scott (2016). "P ≟ NP" (PDF). In Nash, John Forbes Jr.; Rassias, Michael Th. (eds.). Open Problems in Mathematics. Springer International Publishing. pp. 1–122. doi:10.1007/978-3-319-32162-2_1. ISBN   9783319321622. See Section 2.2.4 Factoring and Graph Isomorphism, pp. 19–20 of book (pp. 17–18 of linked version).
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.