Set notation

Sets are fundamental objects in mathematics. Intuitively, a set is merely a collection of elements or members. There are various conventions for textually denoting sets. In any particular situation, an author typically chooses from among these conventions depending on which properties of the set are most relevant to the immediate context or on which perspective is most useful.

Denoting a set as an object

Where it is desirable to refer to a set as an indivisible entity, one typically denotes it by a single capital letter. In referring to an arbitrary, generic set, a typical notational choice is S. When several sets are being discussed simultaneously, they are often denoted by the first few capitals: A, B, C, and so forth. By convention, particular symbols are reserved for the most important sets of numbers:

∅ – empty set (also ${\displaystyle \emptyset }$ or ${\displaystyle \varnothing }$ or {} are common)

N – natural numbers

Z – integers (from Zahl, German for number ).

Q – rational numbers (from quotient )

R – real numbers

C – complex numbers

Some authors use the blackboard bold font for these particular sets (${\displaystyle \mathbb {C} }$, ${\displaystyle \mathbb {N} }$, etc.). This usage is widely accepted in handwriting, but some mathematicians, and such experts on mathematical typography as Donald Knuth, advise against its use in print. ^[1]

Focusing on the membership of a set

In many contexts one is interested more in the elements that constitute the set than in the single entity comprising those elements, for instance where stating an extensional definition of the set. Here the elements, whether expressed discretely or in some aggregate manner, are enclosed in braces.

The simplest notational approach of this type, which is feasible only for fairly small sets, is to enumerate the elements exhaustively. Thus the set of suits in a standard deck of playing cards is denoted by {♠, ♦, ♥, ♣} and the set of even prime numbers is denoted by {2}. This approach also provides the notation {} for the empty set.

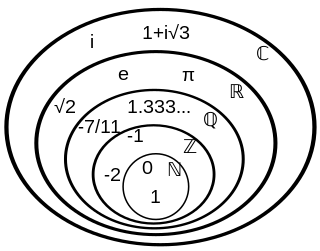
The semantics of the term set imposes certain syntactic constraints on these notations. The only information that is fundamental for a set is which particular objects are, or are not, elements. As a result, the order in which elements appear in an enumeration is irrelevant: {π, 6, 1/2} and {1/2, π, 6} are two enumerations of the same set. Likewise, repeated mention of an element is also irrelevant, so {1, 2, 2, 3, 3, 3} = {1, 2, 3}. To deal with collections for which members' multiplicity is significant, there is a generalization of sets called multisets .

A variant of this explicitly exhaustive enumeration uses ranges of elements and features the ellipsis. For example, the set of the first ten natural numbers can be written as {1, ..., 10}. Here, of course, the ellipsis means "and so forth." Wherever an ellipsis is used to denote a range, it is punctuated as though it were an element of the set. If either extreme of a range is indeterminate, it may be denoted by a mathematical expression giving a formula to compute it. As an example, if n is known from context to be a positive integer, then the set of the first n perfect squares may be denoted by {1, 4, ..., n²}.

In general, if ${\displaystyle n}$ is a natural number, then ${\displaystyle \{1,\dots ,n\}}$ denotes the set ${\displaystyle \{i\in \mathbb {N} \mid 1\leq i\leq n\}}$. A subtle special is ${\displaystyle n=0}$, in which ${\displaystyle \{1,\dots ,0\}}$ is the empty set ${\displaystyle \emptyset }$.

Some infinite sets, too, can be represented in this way. An example is denoting the set of natural numbers (for which one notation described above is N) by {1, 2, 3, ...}. In cases where the infinitely repeating pattern is not obvious, one can insert an expression to represent a generic element of the set, as with {0, 1, 3, ..., k(k-1)/2, ...}.

A more powerful mechanism for denoting a set in terms of its elements is set-builder notation. Here the general pattern is {x : P(x)}, which denotes the set of all elements x (from some universal set) for which the assertion P(x) about x is true. For example, when understood as a set of points, the circle with radius r and center (a, b), may be denoted as {(u, v) : (u−a)² + (v-b)² = r²}.

A notable exception to the braces notation is used to express intervals on the real line. It makes use of the fact that any such interval is completely determined by its left and right endpoints: the unit interval, for instance, is the set of reals between 0 and 1 (inclusive). The convention for denoting intervals uses brackets and parentheses, depending as the corresponding endpoint is included in or excluded from the set, respectively. Thus the set of reals with absolute value less than one is denoted by (−1, 1) — This is very different from the ordered pair with first entry −1 and second entry 1. As other examples, the set of reals x that satisfy 2 < x ≤ 5 is denoted by (2, 5], and the set of nonnegative reals is denoted by [0, ∞).

Metaphor in denoting sets

Since so much of mathematics consists in discovering and exploiting patterns, it is perhaps not surprising that there should have arisen various set-denotational conventions that strike practitioners as obvious or natural—if sometimes only once the pattern has been pointed out.

One class consists of those notations deriving the symbol for a set from the algebraic form of a representative element of the set. As an example, consider the set of even numbers. Since a number b is even precisely if there exists some integer a such that b = 2a, the following variation on set-builder notation could be used to denote this set: {2a : a∈Z} (compare this with the formal set-builder notation: {b∈Z : ∃ a∈Z: b = 2a}). Alternatively, a single symbol for the set of even numbers is 2Z. Likewise, since any odd number must have the form 2a + 1 for some integer a, the set of odd numbers may be denoted 2Z+1.

A second class is based on a strong logical relationship between a set and a particular integer. One example is the bracket notation, in which the set {1, ..., n} of the first n positive integers is denoted by [n]. (As a related point, when endowed with the standard less-than-or-equal relation ≤, the set [n] yields the poset denoted by n.) Another example arises from modular arithmetic, where equivalence classes are denoted by ${\displaystyle {\bar {a}}_{n}}$, which may be understood to represent the set of integers that leave remainder a on division by n. Thus yet another notation for the set of even numbers is ${\displaystyle {\bar {0}}_{2}}$.

Another set-denotational convention that relies on metaphor comes from enumerative combinatorics. It derives a symbol for a set S from an expression for the set's cardinality, or size, |S|. Perhaps the simplest and best known example is the Cartesian product of sets A and B, which is the set {(a, b) : a∈A, b∈B}. Since, in this set, every element of A gets paired exactly once with every element of B, its cardinality is |A| × |B|. For this reason, the set is denoted by A×B. In fact, that same fact about its cardinality is why this set is called a product.

There are many other examples of this convention. One is the set of functions from set A to set B. When A and B are finite, specifying any such function amounts to choosing for each element of A which element of B should be its image. So, the number of these functions is |B|^|A|. Thus, one denotes the set of all functions from A to B as B^A. Another example is the power set of a set S, which, having cardinality 2^|S|, is denoted by 2^S. Note, though, that since any subset of S may be seen as a function assigning to each element of S one or the other element of {include, exclude}, the notation 2^S may be seen as a special case of B^A. The cardinality metaphor has also been used to derive from the standard notation for binomial coefficients the notation ${\displaystyle {\tbinom {X}{k}}}$ for the set of all k-element subsets of a set X. An alternative notation to denote the all ${\displaystyle k}$-subsets of ${\displaystyle X}$ is ${\displaystyle [X]^{k}}$

An example where this cardinality-based convention appears not to have been used yet is X! to denote the set of all permutations of a set X. Since it is usually seen as the underlying set of a symmetric group, this set is typically denoted by a symbol for the group itself, either S_X or Sym(X).

Other conventions

Further conventions are also sometimes seen, including one based on relations. For a relation R on a set S, one may denote the set of objects related by R to some element x of S by S_R(x). So from the notation | for the divides relation of number theory, one may denote the set of factors of an integer n by Z_|(n). Similarly, a subset of X is a principal lower set of a poset (X, ≤) precisely if it can be denoted by X_≤(x) for some x in X. And since ~ is the symbol for the adjacency relation, the subset of a collection W of vertices of a graph that includes exactly those adjacent to a vertex v (namely, the intersection of W with the open neighborhood of v) may be denoted by W_~(v).

See also

• List of mathematical symbols
• List (computing)
• Sequence
• Set-builder notation
• Mathematical notation
• Ordinal notation
• Presentations of groups  – features syntax roughly analogous to that of set-builder notation

References

1. Krantz, S., Handbook of Typography for the Mathematical Sciences, Chapman & Hall/CRC, Boca Raton, Florida, 2001, p. 35.