
Magnetohydrodynamics is a model of electrically conducting fluids that treats all interpenetrating particle species together as a single continuous medium. It is primarily concerned with the low-frequency, large-scale, magnetic behavior in plasmas and liquid metals and has applications in numerous fields including geophysics, astrophysics, and engineering.
Magnetoresistance is the tendency of a material to change the value of its electrical resistance in an externally-applied magnetic field. There are a variety of effects that can be called magnetoresistance. Some occur in bulk non-magnetic metals and semiconductors, such as geometrical magnetoresistance, Shubnikov–de Haas oscillations, or the common positive magnetoresistance in metals. Other effects occur in magnetic metals, such as negative magnetoresistance in ferromagnets or anisotropic magnetoresistance (AMR). Finally, in multicomponent or multilayer systems, giant magnetoresistance (GMR), tunnel magnetoresistance (TMR), colossal magnetoresistance (CMR), and extraordinary magnetoresistance (EMR) can be observed.

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.
In plasma physics, an Alfvén wave, named after Hannes Alfvén, is a type of plasma wave in which ions oscillate in response to a restoring force provided by an effective tension on the magnetic field lines.

Magnetic reconnection is a physical process occurring in electrically conducting plasmas, in which the magnetic topology is rearranged and magnetic energy is converted to kinetic energy, thermal energy, and particle acceleration. Magnetic reconnection involves plasma flows at a substantial fraction of the Alfvén wave speed, which is the fundamental speed for mechanical information flow in a magnetized plasma.
In physics, magnetosonic waves, also known as magnetoacoustic waves, are low-frequency compressive waves driven by mutual interaction between an electrically conducting fluid and a magnetic field. They are associated with compression and rarefaction of both the fluid and the magnetic field, as well as with an effective tension that acts to straighten bent magnetic field lines. The properties of magnetosonic waves are highly dependent on the angle between the wavevector and the equilibrium magnetic field and on the relative importance of fluid and magnetic processes in the medium. They only propagate with frequencies much smaller than the ion cyclotron or ion plasma frequencies of the medium, and they are nondispersive at small amplitudes.
The Vlasov equation is a differential equation describing time evolution of the distribution function of plasma consisting of charged particles with long-range interaction, such as the Coulomb interaction. The equation was first suggested for the description of plasma by Anatoly Vlasov in 1938 and later discussed by him in detail in a monograph.
The Grad–Shafranov equation is the equilibrium equation in ideal magnetohydrodynamics (MHD) for a two dimensional plasma, for example the axisymmetric toroidal plasma in a tokamak. This equation takes the same form as the Hicks equation from fluid dynamics. This equation is a two-dimensional, nonlinear, elliptic partial differential equation obtained from the reduction of the ideal MHD equations to two dimensions, often for the case of toroidal axisymmetry. Taking as the cylindrical coordinates, the flux function is governed by the equation,

In physics, magnetic pressure is an energy density associated with a magnetic field. In SI units, the energy density of a magnetic field with strength can be expressed as
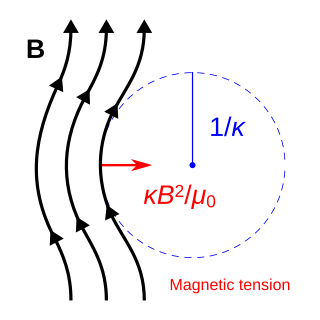
In physics, magnetic tension is a restoring force with units of force density that acts to straighten bent magnetic field lines. In SI units, the force density exerted perpendicular to a magnetic field can be expressed as

A flux tube is a generally tube-like (cylindrical) region of space containing a magnetic field, B, such that the cylindrical sides of the tube are everywhere parallel to the magnetic field lines. It is a graphical visual aid for visualizing a magnetic field. Since no magnetic flux passes through the sides of the tube, the flux through any cross section of the tube is equal, and the flux entering the tube at one end is equal to the flux leaving the tube at the other. Both the cross-sectional area of the tube and the magnetic field strength may vary along the length of the tube, but the magnetic flux inside is always constant.
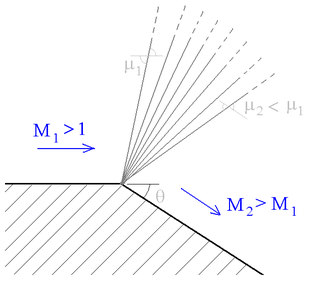
A supersonic expansion fan, technically known as Prandtl–Meyer expansion fan, a two-dimensional simple wave, is a centered expansion process that occurs when a supersonic flow turns around a convex corner. The fan consists of an infinite number of Mach waves, diverging from a sharp corner. When a flow turns around a smooth and circular corner, these waves can be extended backwards to meet at a point.
In plasma physics, the Hasegawa–Mima equation, named after Akira Hasegawa and Kunioki Mima, is an equation that describes a certain regime of plasma, where the time scales are very fast, and the distance scale in the direction of the magnetic field is long. In particular the equation is useful for describing turbulence in some tokamaks. The equation was introduced in Hasegawa and Mima's paper submitted in 1977 to Physics of Fluids, where they compared it to the results of the ATC tokamak.
The Chandrasekhar number is a dimensionless quantity used in magnetic convection to represent ratio of the Lorentz force to the viscosity. It is named after the Indian astrophysicist Subrahmanyan Chandrasekhar.

The theory of special relativity plays an important role in the modern theory of classical electromagnetism. It gives formulas for how electromagnetic objects, in particular the electric and magnetic fields, are altered under a Lorentz transformation from one inertial frame of reference to another. It sheds light on the relationship between electricity and magnetism, showing that frame of reference determines if an observation follows electric or magnetic laws. It motivates a compact and convenient notation for the laws of electromagnetism, namely the "manifestly covariant" tensor form.
Coronal seismology is a technique of studying the plasma of the Sun's corona with the use of magnetohydrodynamic (MHD) waves and oscillations. Magnetohydrodynamics studies the dynamics of electrically conducting fluids - in this case the fluid is the coronal plasma. Observed properties of the waves (e.g. period, wavelength, amplitude, temporal and spatial signatures, characteristic scenarios of the wave evolution, combined with a theoretical modelling of the wave phenomena, may reflect physical parameters of the corona which are not accessible in situ, such as the coronal magnetic field strength and Alfvén velocity and coronal dissipative coefficients. Originally, the method of MHD coronal seismology was suggested by Y. Uchida in 1970 for propagating waves, and B. Roberts et al. in 1984 for standing waves, but was not practically applied until the late 90s due to a lack of necessary observational resolution. Philosophically, coronal seismology is similar to the Earth's seismology, helioseismology, and MHD spectroscopy of laboratory plasma devices. In all these approaches, waves of various kind are used to probe a medium.
The electrothermal instability is a magnetohydrodynamic (MHD) instability appearing in magnetized non-thermal plasmas used in MHD converters. It was first theoretically discovered in 1962 and experimentally measured into a MHD generator in 1963 by Evgeny Velikhov.
"This paper shows that it is possible to assert sufficiently specifically that the ionization instability is the number one problem for the utilization of a plasma with hot electrons."
Magnetohydrodynamic turbulence concerns the chaotic regimes of magnetofluid flow at high Reynolds number. Magnetohydrodynamics (MHD) deals with what is a quasi-neutral fluid with very high conductivity. The fluid approximation implies that the focus is on macro length-and-time scales which are much larger than the collision length and collision time respectively.
In ideal magnetohydrodynamics, Alfvén's theorem, or the frozen-in flux theorem, states that electrically conducting fluids and embedded magnetic fields are constrained to move together in the limit of large magnetic Reynolds numbers. It is named after Hannes Alfvén, who put the idea forward in 1943.






















