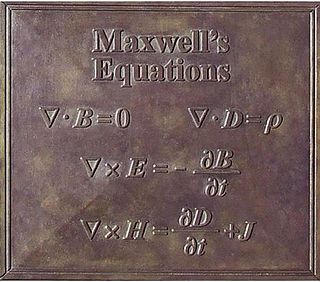An electromagnetic field is a physical field, mathematical functions of position and time, representing the influences on and due to electric charges. The field at any point in space and time can be regarded as a combination of an electric field and a magnetic field. Because of the interrelationship between the fields, a disturbance in the electric field can create a disturbance in the magnetic field which in turn affects the electric field, leading to an oscillation that propagates through space, known as an electromagnetic wave.

In physics, specifically in electromagnetism, the Lorentz force law is the combination of electric and magnetic force on a point charge due to electromagnetic fields. The Lorentz force, on the other hand, is a physical effect that occurs in the vicinity of electrically neutral, current-carrying conductors causing moving electrical charges to experience a magnetic force.
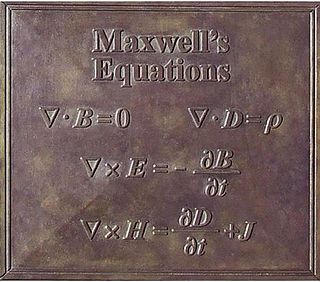
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, electric and magnetic circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar, etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern form of the equations in their most common formulation is credited to Oliver Heaviside.

A magnetic field is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, electric currents, and electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, called a vector field.

In physics, specifically electromagnetism, the Biot–Savart law is an equation describing the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and proximity of the electric current.

In classical electromagnetism, Ampère's circuital law relates the circulation of a magnetic field around a closed loop to the electric current passing through the loop.

In electromagnetism, the magnetic moment or magnetic dipole moment is the combination of strength and orientation of a magnet or other object or system that exerts a magnetic field. The magnetic dipole moment of an object determines the magnitude of torque the object experiences in a given magnetic field. When the same magnetic field is applied, objects with larger magnetic moments experience larger torques. The strength of this torque depends not only on the magnitude of the magnetic moment but also on its orientation relative to the direction of the magnetic field. Its direction points from the south pole to north pole of the magnet.

In electromagnetism, displacement current density is the quantity ∂D/∂t appearing in Maxwell's equations that is defined in terms of the rate of change of D, the electric displacement field. Displacement current density has the same units as electric current density, and it is a source of the magnetic field just as actual current is. However it is not an electric current of moving charges, but a time-varying electric field. In physical materials, there is also a contribution from the slight motion of charges bound in atoms, called dielectric polarization.
"A Dynamical Theory of the Electromagnetic Field" is a paper by James Clerk Maxwell on electromagnetism, published in 1865. In the paper, Maxwell derives an electromagnetic wave equation with a velocity for light in close agreement with measurements made by experiment, and deduces that light is an electromagnetic wave.

In classical electromagnetism, magnetic vector potential is the vector quantity defined so that its curl is equal to the magnetic field: . Together with the electric potential φ, the magnetic vector potential can be used to specify the electric field E as well. Therefore, many equations of electromagnetism can be written either in terms of the fields E and B, or equivalently in terms of the potentials φ and A. In more advanced theories such as quantum mechanics, most equations use potentials rather than fields.
A classical field theory is a physical theory that predicts how one or more fields in physics interact with matter through field equations, without considering effects of quantization; theories that incorporate quantum mechanics are called quantum field theories. In most contexts, 'classical field theory' is specifically intended to describe electromagnetism and gravitation, two of the fundamental forces of nature.
In differential geometry, the four-gradient is the four-vector analogue of the gradient from vector calculus.
In electromagnetism, the Lorenz gauge condition or Lorenz gauge is a partial gauge fixing of the electromagnetic vector potential by requiring The name is frequently confused with Hendrik Lorentz, who has given his name to many concepts in this field. The condition is Lorentz invariant. The Lorenz gauge condition does not completely determine the gauge: one can still make a gauge transformation where is the four-gradient and is any harmonic scalar function: that is, a scalar function obeying the equation of a massless scalar field.

In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field configurations. Any two detailed configurations in the same equivalence class are related by a certain transformation, equivalent to a shear along unphysical axes in configuration space. Most of the quantitative physical predictions of a gauge theory can only be obtained under a coherent prescription for suppressing or ignoring these unphysical degrees of freedom.

In plasma physics, a force-free magnetic field is a magnetic field in which the Lorentz force is equal to zero and the magnetic pressure greatly exceeds the plasma pressure such that non-magnetic forces can be neglected. For a force-free field, the electric current density is either zero or parallel to the magnetic field.

A current sheet is an electric current that is confined to a surface, rather than being spread through a volume of space. Current sheets feature in magnetohydrodynamics (MHD), a model of electrically conductive fluids: if there is an electric current through part of the volume of such a fluid, magnetic forces tend to expel it from the fluid, compressing the current into thin layers that pass through the volume.

The Maxwell stress tensor is a symmetric second-order tensor in three dimensions that is used in classical electromagnetism to represent the interaction between electromagnetic forces and mechanical momentum. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impractically difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand.
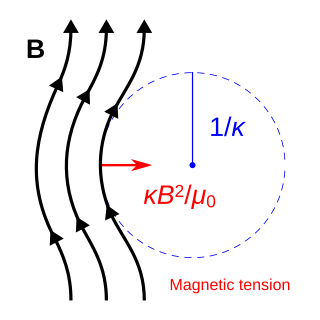
In physics, magnetic tension is a restoring force with units of force density that acts to straighten bent magnetic field lines. In SI units, the force density exerted perpendicular to a magnetic field can be expressed as

A flux tube is a generally tube-like (cylindrical) region of space containing a magnetic field, B, such that the cylindrical sides of the tube are everywhere parallel to the magnetic field lines. It is a graphical visual aid for visualizing a magnetic field. Since no magnetic flux passes through the sides of the tube, the flux through any cross section of the tube is equal, and the flux entering the tube at one end is equal to the flux leaving the tube at the other. Both the cross-sectional area of the tube and the magnetic field strength may vary along the length of the tube, but the magnetic flux inside is always constant.
Magnets exert forces and torques on each other through the interaction of their magnetic fields. The forces of attraction and repulsion are a result of these interactions. The magnetic field of each magnet is due to microscopic currents of electrically charged electrons orbiting nuclei and the intrinsic magnetism of fundamental particles that make up the material. Both of these are modeled quite well as tiny loops of current called magnetic dipoles that produce their own magnetic field and are affected by external magnetic fields. The most elementary force between magnets is the magnetic dipole–dipole interaction. If all magnetic dipoles for each magnet are known then the net force on both magnets can be determined by summing all the interactions between the dipoles of the first magnet and the dipoles of the second magnet.