
In physics, the Coriolis force is an inertial force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term Coriolis force began to be used in connection with meteorology.

Pressure is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure is the pressure relative to the ambient pressure.
Atmospheric pressure, also known as air pressure or barometric pressure, is the pressure within the atmosphere of Earth. The standard atmosphere is a unit of pressure defined as 101,325 Pa (1,013.25 hPa), which is equivalent to 1,013.25 millibars, 760 mm Hg, 29.9212 inches Hg, or 14.696 psi. The atm unit is roughly equivalent to the mean sea-level atmospheric pressure on Earth; that is, the Earth's atmospheric pressure at sea level is approximately 1 atm.
Geopotential height or geopotential altitude is a vertical coordinate referenced to Earth's mean sea level that represents the work involved in lifting one unit of mass over one unit of length through a hypothetical space in which the acceleration of gravity is assumed constant. In SI units, a geopotential height difference of one meter implies the vertical transport of a parcel of one kilogram; adopting the standard gravity value, it corresponds to a constant work or potential energy difference of 9.80665 joules.
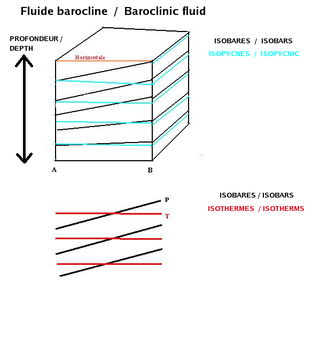
In fluid dynamics, the baroclinity of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid. In meteorology a baroclinic flow is one in which the density depends on both temperature and pressure. A simpler case, barotropic flow, allows for density dependence only on pressure, so that the curl of the pressure-gradient force vanishes.

Wind shear, sometimes referred to as wind gradient, is a difference in wind speed and/or direction over a relatively short distance in the atmosphere. Atmospheric wind shear is normally described as either vertical or horizontal wind shear. Vertical wind shear is a change in wind speed or direction with a change in altitude. Horizontal wind shear is a change in wind speed with a change in lateral position for a given altitude.
The primitive equations are a set of nonlinear partial differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations:
- A continuity equation: Representing the conservation of mass.
- Conservation of momentum: Consisting of a form of the Navier–Stokes equations that describe hydrodynamical flow on the surface of a sphere under the assumption that vertical motion is much smaller than horizontal motion (hydrostasis) and that the fluid layer depth is small compared to the radius of the sphere
- A thermal energy equation: Relating the overall temperature of the system to heat sources and sinks

Fluid statics or hydrostatics is the branch of fluid mechanics that studies fluids at hydrostatic equilibrium and "the pressure in a fluid or exerted by a fluid on an immersed body".
A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature spatial gradient is a vector quantity with dimension of temperature difference per unit length. The SI unit is kelvin per meter (K/m).
Numerical weather prediction (NWP) uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic results. A number of global and regional forecast models are run in different countries worldwide, using current weather observations relayed from radiosondes, weather satellites and other observing systems as inputs.

In atmospheric science, the thermal wind is the vector difference between the geostrophic wind at upper altitudes minus that at lower altitudes in the atmosphere. It is the hypothetical vertical wind shear that would exist if the winds obey geostrophic balance in the horizontal, while pressure obeys hydrostatic balance in the vertical. The combination of these two force balances is called thermal wind balance, a term generalizable also to more complicated horizontal flow balances such as gradient wind balance.

Hydraulic head or piezometric head is a specific measurement of liquid pressure above a vertical datum.

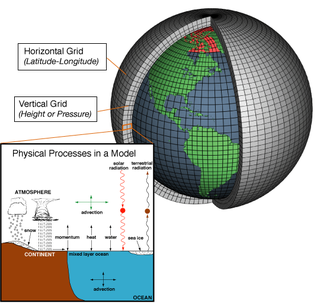
In atmospheric science, an atmospheric model is a mathematical model constructed around the full set of primitive, dynamical equations which govern atmospheric motions. It can supplement these equations with parameterizations for turbulent diffusion, radiation, moist processes, heat exchange, soil, vegetation, surface water, the kinematic effects of terrain, and convection. Most atmospheric models are numerical, i.e. they discretize equations of motion. They can predict microscale phenomena such as tornadoes and boundary layer eddies, sub-microscale turbulent flow over buildings, as well as synoptic and global flows. The horizontal domain of a model is either global, covering the entire Earth, or regional (limited-area), covering only part of the Earth. The different types of models run are thermotropic, barotropic, hydrostatic, and nonhydrostatic. Some of the model types make assumptions about the atmosphere which lengthens the time steps used and increases computational speed.
In fluid mechanics, potential vorticity (PV) is a quantity which is proportional to the dot product of vorticity and stratification. This quantity, following a parcel of air or water, can only be changed by diabatic or frictional processes. It is a useful concept for understanding the generation of vorticity in cyclogenesis, especially along the polar front, and in analyzing flow in the ocean.
In atmospheric science, balanced flow is an idealisation of atmospheric motion. The idealisation consists in considering the behaviour of one isolated parcel of air having constant density, its motion on a horizontal plane subject to selected forces acting on it and, finally, steady-state conditions.

Atmospheric instability is a condition where the Earth's atmosphere is considered to be unstable and as a result local weather is highly variable through distance and time. Atmospheric stability is a measure of the atmosphere's tendency to discourage vertical motion, and vertical motion is directly correlated to different types of weather systems and their severity. In unstable conditions, a lifted thing, such as a parcel of air will be warmer than the surrounding air. Because it is warmer, it is less dense and is prone to further ascent.
The omega equation is a culminating result in synoptic-scale meteorology. It is an elliptic partial differential equation, named because its left-hand side produces an estimate of vertical velocity, customarily expressed by symbol , in a pressure coordinate measuring height the atmosphere. Mathematically, , where represents a material derivative. The underlying concept is more general, however, and can also be applied to the Boussinesq fluid equation system where vertical velocity is in altitude coordinate z.
Vertical pressure variation is the variation in pressure as a function of elevation. Depending on the fluid in question and the context being referred to, it may also vary significantly in dimensions perpendicular to elevation as well, and these variations have relevance in the context of pressure gradient force and its effects. However, the vertical variation is especially significant, as it results from the pull of gravity on the fluid; namely, for the same given fluid, a decrease in elevation within it corresponds to a taller column of fluid weighing down on that point.

This glossary of meteorology is a list of terms and concepts relevant to meteorology and atmospheric science, their sub-disciplines, and related fields.
Atmospheric circulation of a planet is largely specific to the planet in question and the study of atmospheric circulation of exoplanets is a nascent field as direct observations of exoplanet atmospheres are still quite sparse. However, by considering the fundamental principles of fluid dynamics and imposing various limiting assumptions, a theoretical understanding of atmospheric motions can be developed. This theoretical framework can also be applied to planets within the Solar System and compared against direct observations of these planets, which have been studied more extensively than exoplanets, to validate the theory and understand its limitations as well.










