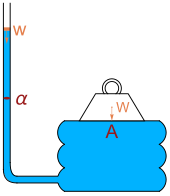
Pressure is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure is the pressure relative to the ambient pressure.

Relative density, also called specific gravity, is a dimensionless quantity defined as the ratio of the density of a substance to the density of a given reference material. Specific gravity for liquids is nearly always measured with respect to water at its densest ; for gases, the reference is air at room temperature. The term "relative density" is preferred in SI, whereas the term "specific gravity" is gradually being abandoned.
Atmospheric pressure, also known as air pressure or barometric pressure, is the pressure within the atmosphere of Earth. The standard atmosphere is a unit of pressure defined as 101,325 Pa (1,013.25 hPa), which is equivalent to 1,013.25 millibars, 760 mm Hg, 29.9212 inches Hg, or 14.696 psi. The atm unit is roughly equivalent to the mean sea-level atmospheric pressure on Earth; that is, the Earth's atmospheric pressure at sea level is approximately 1 atm.

In fluid mechanics, hydrostatic equilibrium is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planetary physics of Earth, the pressure-gradient force prevents gravity from collapsing the planetary atmosphere into a thin, dense shell, whereas gravity prevents the pressure-gradient force from diffusing the atmosphere into outer space. In general, it is what causes objects in space to be spherical.

Bernoulli's principle is a key concept in fluid dynamics that relates pressure, speed and height. Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or the fluid's potential energy. The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book Hydrodynamica in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form.
Geopotential height or geopotential altitude is a vertical coordinate referenced to Earth's mean sea level that represents the work involved in lifting one unit of mass over one unit of length through a hypothetical space in which the acceleration of gravity is assumed constant. In SI units, a geopotential height difference of one meter implies the vertical transport of a parcel of one kilogram; adopting the standard gravity value, it corresponds to a constant work or potential energy difference of 9.80665 joules.

Buoyancy, or upthrust, is an upward force exerted by a fluid that opposes the weight of a partially or fully immersed object. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the displaced fluid.
Equivalent potential temperature, commonly referred to as theta-e, is a quantity that is conserved during changes to an air parcel's pressure, even if water vapor condenses during that pressure change. It is therefore more conserved than the ordinary potential temperature, which remains constant only for unsaturated vertical motions.
Archimedes' principle states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse.
The density of air or atmospheric density, denoted ρ, is the mass per unit volume of Earth's atmosphere. Air density, like air pressure, decreases with increasing altitude. It also changes with variations in atmospheric pressure, temperature and humidity. At 101.325 kPa (abs) and 20 °C, air has a density of approximately 1.204 kg/m3 (0.0752 lb/cu ft), according to the International Standard Atmosphere (ISA). At 101.325 kPa (abs) and 15 °C (59 °F), air has a density of approximately 1.225 kg/m3 (0.0765 lb/cu ft), which is about 1⁄800 that of water, according to the International Standard Atmosphere (ISA). Pure liquid water is 1,000 kg/m3 (62 lb/cu ft).

Fluid statics or hydrostatics is the branch of fluid mechanics that studies fluids at hydrostatic equilibrium and "the pressure in a fluid or exerted by a fluid on an immersed body".
The barometric formula is a formula used to model how the pressure of the air changes with altitude.

In atmospheric science, the thermal wind is the vector difference between the geostrophic wind at upper altitudes minus that at lower altitudes in the atmosphere. It is the hypothetical vertical wind shear that would exist if the winds obey geostrophic balance in the horizontal, while pressure obeys hydrostatic balance in the vertical. The combination of these two force balances is called thermal wind balance, a term generalizable also to more complicated horizontal flow balances such as gradient wind balance.

Hydraulic head or piezometric head is a specific measurement of liquid pressure above a vertical datum.

In atmospheric, earth, and planetary sciences, a scale height, usually denoted by the capital letter H, is a distance over which a physical quantity decreases by a factor of e.
A reference atmospheric model describes how the ideal gas properties of an atmosphere change, primarily as a function of altitude, and sometimes also as a function of latitude, day of year, etc. A static atmospheric model has a more limited domain, excluding time. A standard atmosphere is defined by the World Meteorological Organization as "a hypothetical vertical distribution of atmospheric temperature, pressure and density which, by international agreement, is roughly representative of year-round, midlatitude conditions."
In fluid dynamics, dynamic pressure is the quantity defined by:
The hypsometric equation, also known as the thickness equation, relates an atmospheric pressure ratio to the equivalent thickness of an atmospheric layer considering the layer mean of virtual temperature, gravity, and occasionally wind. It is derived from the hydrostatic equation and the ideal gas law.

The capillary length or capillary constant, is a length scaling factor that relates gravity and surface tension. It is a fundamental physical property that governs the behavior of menisci, and is found when body forces (gravity) and surface forces are in equilibrium.
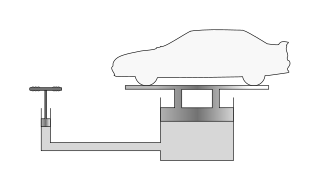
Pascal's law is a principle in fluid mechanics given by Blaise Pascal that states that a pressure change at any point in a confined incompressible fluid is transmitted throughout the fluid such that the same change occurs everywhere. The law was established by French mathematician Blaise Pascal in 1653 and published in 1663.