The barotropic vorticity equation assumes the atmosphere is nearly barotropic, which means that the direction and speed of the geostrophic wind are independent of height. In other words, there is no vertical wind shear of the geostrophic wind. It also implies that thickness contours are parallel to upper level height contours. In this type of atmosphere, high and low pressure areas are centers of warm and cold temperature anomalies. Warm-core highs and cold-core lows have strengthening winds with height, with the reverse true for cold-core highs and warm-core lows.

A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete trajectory is defined by position and momentum, simultaneously.
In fluid dynamics, Stokes' law is an empirical law for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a viscous fluid. It was derived by George Gabriel Stokes in 1851 by solving the Stokes flow limit for small Reynolds numbers of the Navier–Stokes equations.
Equivalent potential temperature, commonly referred to as theta-e, is a quantity that is conserved during changes to an air parcel's pressure, even if water vapor condenses during that pressure change. It is therefore more conserved than the ordinary potential temperature, which remains constant only for unsaturated vertical motions.
The primitive equations are a set of nonlinear partial differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations:
- A continuity equation: Representing the conservation of mass.
- Conservation of momentum: Consisting of a form of the Navier–Stokes equations that describe hydrodynamical flow on the surface of a sphere under the assumption that vertical motion is much smaller than horizontal motion (hydrostasis) and that the fluid layer depth is small compared to the radius of the sphere
- A thermal energy equation: Relating the overall temperature of the system to heat sources and sinks
Rossby waves, also known as planetary waves, are a type of inertial wave naturally occurring in rotating fluids. They were first identified by Sweden-born American meteorologist Carl-Gustaf Arvid Rossby. They are observed in the atmospheres and oceans of Earth and other planets, owing to the rotation of Earth or of the planet involved. Atmospheric Rossby waves on Earth are giant meanders in high-altitude winds that have a major influence on weather. These waves are associated with pressure systems and the jet stream. Oceanic Rossby waves move along the thermocline: the boundary between the warm upper layer and the cold deeper part of the ocean.

In meteorology, lee waves are atmospheric stationary waves. The most common form is mountain waves, which are atmospheric internal gravity waves. These were discovered in 1933 by two German glider pilots, Hans Deutschmann and Wolf Hirth, above the Krkonoše. They are periodic changes of atmospheric pressure, temperature and orthometric height in a current of air caused by vertical displacement, for example orographic lift when the wind blows over a mountain or mountain range. They can also be caused by the surface wind blowing over an escarpment or plateau, or even by upper winds deflected over a thermal updraft or cloud street.

Projectile motion is a form of motion experienced by an object or particle that is projected in a gravitational field, such as from Earth's surface, and moves along a curved path under the action of gravity only. In the particular case of projectile motion on Earth, most calculations assume the effects of air resistance are passive and negligible. The curved path of objects in projectile motion was shown by Galileo to be a parabola, but may also be a straight line in the special case when it is thrown directly upward or downward. The study of such motions is called ballistics, and such a trajectory is a ballistic trajectory. The only force of mathematical significance that is actively exerted on the object is gravity, which acts downward, thus imparting to the object a downward acceleration towards the Earth’s center of mass. Because of the object's inertia, no external force is needed to maintain the horizontal velocity component of the object's motion. Taking other forces into account, such as aerodynamic drag or internal propulsion, requires additional analysis. A ballistic missile is a missile only guided during the relatively brief initial powered phase of flight, and whose remaining course is governed by the laws of classical mechanics.

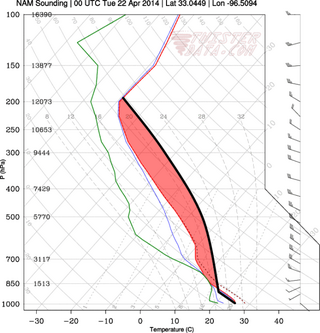
In meteorology, convective available potential energy, is the integrated amount of work that the upward (positive) buoyancy force would perform on a given mass of air if it rose vertically through the entire atmosphere. Positive CAPE will cause the air parcel to rise, while negative CAPE will cause the air parcel to sink. Nonzero CAPE is an indicator of atmospheric instability in any given atmospheric sounding, a necessary condition for the development of cumulus and cumulonimbus clouds with attendant severe weather hazards.

Cyclogenesis is the development or strengthening of cyclonic circulation in the atmosphere. Cyclogenesis is an umbrella term for at least three different processes, all of which result in the development of some sort of cyclone, and at any size from the microscale to the synoptic scale.
The potential temperature of a parcel of fluid at pressure is the temperature that the parcel would attain if adiabatically brought to a standard reference pressure , usually 1,000 hPa (1,000 mb). The potential temperature is denoted and, for a gas well-approximated as ideal, is given by

Convective inhibition is a numerical measure in meteorology that indicates the amount of energy that will prevent an air parcel from rising from the surface to the level of free convection.
In atmospheric dynamics, oceanography, asteroseismology and geophysics, the Brunt–Väisälä frequency, or buoyancy frequency, is a measure of the stability of a fluid to vertical displacements such as those caused by convection. More precisely it is the frequency at which a vertically displaced parcel will oscillate within a statically stable environment. It is named after David Brunt and Vilho Väisälä. It can be used as a measure of atmospheric stratification.
In meteorology, convective instability or stability of an air mass refers to its ability to resist vertical motion. A stable atmosphere makes vertical movement difficult, and small vertical disturbances dampen out and disappear. In an unstable atmosphere, vertical air movements tend to become larger, resulting in turbulent airflow and convective activity. Instability can lead to significant turbulence, extensive vertical clouds, and severe weather such as thunderstorms.
In fluid mechanics, potential vorticity (PV) is a quantity which is proportional to the dot product of vorticity and stratification. This quantity, following a parcel of air or water, can only be changed by diabatic or frictional processes. It is a useful concept for understanding the generation of vorticity in cyclogenesis, especially along the polar front, and in analyzing flow in the ocean.

The shallow-water equations (SWE) are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid. The shallow-water equations in unidirectional form are also called Saint-Venant equations, after Adhémar Jean Claude Barré de Saint-Venant.
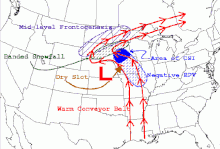
Frontogenesis is a meteorological process of tightening of horizontal temperature gradients to produce fronts. In the end, two types of fronts form: cold fronts and warm fronts. A cold front is a narrow line where temperature decreases rapidly. A warm front is a narrow line of warmer temperatures and essentially where much of the precipitation occurs. Frontogenesis occurs as a result of a developing baroclinic wave. According to Hoskins & Bretherton, there are eight mechanisms that influence temperature gradients: horizontal deformation, horizontal shearing, vertical deformation, differential vertical motion, latent heat release, surface friction, turbulence and mixing, and radiation. Semigeostrophic frontogenesis theory focuses on the role of horizontal deformation and shear.
The omega equation is a culminating result in synoptic-scale meteorology. It is an elliptic partial differential equation, named because its left-hand side produces an estimate of vertical velocity, customarily expressed by symbol , in a pressure coordinate measuring height the atmosphere. Mathematically, , where represents a material derivative. The underlying concept is more general, however, and can also be applied to the Boussinesq fluid equation system where vertical velocity is in altitude coordinate z.
In fluid dynamics, the Burgers vortex or Burgers–Rott vortex is an exact solution to the Navier–Stokes equations governing viscous flow, named after Jan Burgers and Nicholas Rott. The Burgers vortex describes a stationary, self-similar flow. An inward, radial flow, tends to concentrate vorticity in a narrow column around the symmetry axis. At the same time, viscous diffusion tends to spread the vorticity. The stationary Burgers vortex arises when the two effects balance.
A baroclinic instability is a fluid dynamical instability of fundamental importance in the atmosphere and ocean. It can lead to the formation of transient mesoscale eddies, with a horizontal scale of 10-100 km. In contrast, flows on the largest scale in the ocean are described as ocean currents, the largest scale eddies are mostly created by shearing of two ocean currents and static mesoscale eddies are formed by the flow around an obstacle (as seen in the animation on eddy. Mesoscale eddies are circular currents with swirling motion and account for approximately 90% of the ocean's total kinetic energy. Therefore, they are key in mixing and transport of for example heat, salt and nutrients.