This article needs additional citations for verification .(April 2022) |



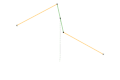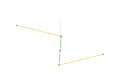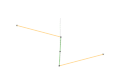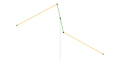
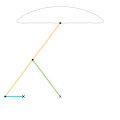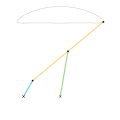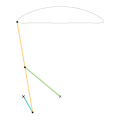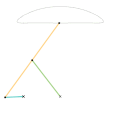
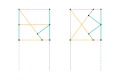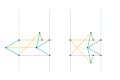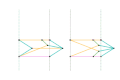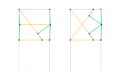
Parts of the same color are the same dimensions.

Links of the same color are the same length.
A straight-line mechanism is a mechanism that converts any type of rotary or angular motion to perfect or near-perfect straight-line motion, or vice versa. Straight-line motion is linear motion of definite length or "stroke", every forward stroke being followed by a return stroke, giving reciprocating motion. The first such mechanism, patented in 1784 by James Watt, produced approximate straight-line motion, referred to by Watt as parallel motion.
Contents
- History
- List of linkages
- Approximate straight-line linkages
- Perfect straight-line linkages
- Compound eccentric mechanisms with elliptical motion
- Gallery
- Approximate straight-line linkages 2
- Perfect straight-line linkages 2
- Tusi couple, elliptical motion: versions and inversions
- Compound eccentric mechanisms with elliptical motion 2
- See also
- Notes
- References
- External links
Straight-line mechanisms are used in a variety of applications, such as engines, vehicle suspensions, walking robots, and rover wheels.[ citation needed ]