Related Research Articles

A sphere is a geometrical object in three-dimensional space that is the surface of a ball.

In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.

Surface tension is the tendency of liquid surfaces to shrink into the minimum surface area possible. Surface tension is what allows heavier than water i.e., denser than water objects such as razor blades, insects, to float and slide on a water surface without becoming even partly submerged.
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature.
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology.
In mathematics, the mean curvature of a surface is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space.

Richard Streit Hamilton is Davies Professor of Mathematics at Columbia University. He is known for contributions to geometric analysis and partial differential equations. He made foundational contributions to the theory of the Ricci flow and its use in the resolution of the Poincaré conjecture and geometrization conjecture in the field of geometric topology.

In differential geometry, the Willmore energy is a quantitative measure of how much a given surface deviates from a round sphere. Mathematically, the Willmore energy of a smooth closed surface embedded in three-dimensional Euclidean space is defined to be the integral of the square of the mean curvature minus the Gaussian curvature. It is named after the English geometer Thomas Willmore.

Geometric analysis is a mathematical discipline where tools from differential equations, especially elliptic partial differential equations are used to establish new results in differential geometry and differential topology. The use of linear elliptic PDEs dates at least as far back as Hodge theory. More recently, it refers largely to the use of nonlinear partial differential equations to study geometric and topological properties of spaces, such as submanifolds of Euclidean space, Riemannian manifolds, and symplectic manifolds. This approach dates back to the work by Tibor Radó and Jesse Douglas on minimal surfaces, John Forbes Nash Jr. on isometric embeddings of Riemannian manifolds into Euclidean space, work by Louis Nirenberg on the Minkowski problem and the Weyl problem, and work by Aleksandr Danilovich Aleksandrov and Aleksei Pogorelov on convex hypersurfaces. In the 1980s fundamental contributions by Karen Uhlenbeck, Clifford Taubes, Shing-Tung Yau, Richard Schoen, and Richard Hamilton launched a particularly exciting and productive era of geometric analysis that continues to this day. A celebrated achievement was the solution to the Poincaré conjecture by Grigori Perelman, completing a program initiated and largely carried out by Richard Hamilton.
In mathematics, spaces of non-positive curvature occur in many contexts and form a generalization of hyperbolic geometry. In the category of Riemannian manifolds, one can consider the sectional curvature of the manifold and require that this curvature be everywhere less than or equal to zero. The notion of curvature extends to the category of geodesic metric spaces, where one can use comparison triangles to quantify the curvature of a space; in this context, non-positively curved spaces are known as (locally) CAT(0) spaces.
In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold. Intuitively, a family of surfaces evolves under mean curvature flow if the normal component of the velocity of which a point on the surface moves is given by the mean curvature of the surface. For example, a round sphere evolves under mean curvature flow by shrinking inward uniformly. Except in special cases, the mean curvature flow develops singularities.
In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
The Hawking energy or Hawking mass is one of the possible definitions of mass in general relativity. It is a measure of the bending of ingoing and outgoing rays of light that are orthogonal to a 2-sphere surrounding the region of space whose mass is to be defined.

Herbert Blaine Lawson, Jr. is a mathematician best known for his work in minimal surfaces, calibrated geometry, and algebraic cycles. He is currently a Distinguished Professor of Mathematics at Stony Brook University. He received his PhD from Stanford University in 1969 for work carried out under the supervision of Robert Osserman.
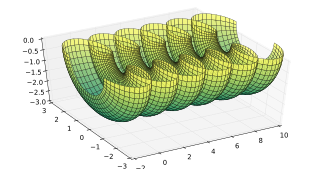
In differential geometry, constant-mean-curvature (CMC) surfaces are surfaces with constant mean curvature. This includes minimal surfaces as a subset, but typically they are treated as special case.

Gerhard Huisken is a German mathematician whose research concerns differential geometry and partial differential equations. He is known for foundational contributions to the theory of the mean curvature flow, including Huisken's monotonicity formula, which is named after him. With Tom Ilmanen, he proved a version of the Riemannian Penrose inequality, which is a special case of the more general Penrose conjecture in general relativity.

A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is the portion with which other materials first interact. The surface of an object is more than "a mere geometric solid", but is "filled with, spread over by, or suffused with perceivable qualities such as color and warmth".

Bang-Yen Chen is a Taiwanese mathematician who works mainly on differential geometry and related subjects. He was a University Distinguished Professor of Michigan State University from 1990 to 2012. After 2012 he became University Distinguished Professor Emeritus.
References
- ↑ Brakke, Kenneth A (1992), "The Surface Evolver" (PDF), Experimental Mathematics , 1 (2): 141–165
- ↑ Carter, Craig (1996), "Surface Evolver" as a Tool for Materials Science Research, National Institute of Standards and Technology