| Truncated triangular trapezohedron | |
|---|---|
 | |
| Type | Truncated trapezohedron |
| Faces | 6 pentagons, 2 triangles |
| Edges | 18 |
| Vertices | 12 |
| Symmetry group | D3d, [2+,6], (2*3) |
| Dual polyhedron | Gyroelongated triangular bipyramid |
| Properties | convex |
In geometry, the truncated triangular trapezohedron is the first in an infinite series of truncated trapezohedra. It has 6 pentagon and 2 triangle faces.
This polyhedron can be constructed by truncating two opposite vertices of a cube, of a trigonal trapezohedron (a convex polyhedron with six congruent rhombus sides, formed by stretching or shrinking a cube along one of its long diagonals), or of a rhombohedron or parallelepiped (less symmetric polyhedra that still have the same combinatorial structure as a cube). In the case of a cube, or of a trigonal trapezohedron where the two truncated vertices are the ones on the stretching axes, the resulting shape has three-fold rotational symmetry.
This polyhedron is sometimes called Dürer's solid, from its appearance in Albrecht Dürer's 1514 engraving Melencolia I . The graph formed by its edges and vertices is called the Dürer graph.
The shape of the solid depicted by Dürer is a subject of some academic debate. [1] According to Lynch (1982), the hypothesis that the shape is a misdrawn truncated cube was promoted by Strauss (1972); however most sources agree that it is the truncation of a rhombohedron. Despite this agreement, the exact geometry of this rhombohedron is the subject of several contradictory theories:
In geometry, an Archimedean solid is one of 13 convex polyhedra whose faces are regular polygons and whose vertices are all symmetric to each other. They were first enumerated by Archimedes. The convex polyhedra with regular faces and symmetric vertices include also the five Platonic solids and the two infinite families of prisms and antiprisms; these are not counted as Archimedean solids. The pseudorhombicuboctahedron has regular faces, and vertices that are symmetric in a weaker sense; it is also not generally counted as an Archimedean solid. The Archimedean solids are a subset of the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices.
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.
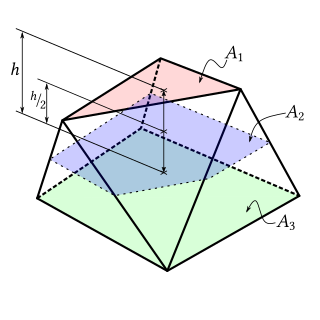
In geometry, a prismatoid is a polyhedron whose vertices all lie in two parallel planes. Its lateral faces can be trapezoids or triangles. If both planes have the same number of vertices, and the lateral faces are either parallelograms or trapezoids, it is called a prismoid.
In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.
In geometry, a cuboid is a hexahedron, a six-faced solid. Its faces are quadrilaterals. Cuboid means "like a cube". A cuboid is like a cube in the sense that by adjusting the lengths of the edges or the angles between faces a cuboid can be transformed into a cube. In mathematical language a cuboid is a convex polyhedron whose polyhedral graph is the same as that of a cube.
In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle, and the latter sometimes refers specifically to a rhombus with a 45° angle.
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.
In geometry, the rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron. It is a zonohedron.
In geometry, an n-gonaltrapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.
In geometry, a rhombohedron is a three-dimensional figure with six faces which are rhombi. It is a special case of a parallelepiped where all edges are the same length. It can be used to define the rhombohedral lattice system, a honeycomb with rhombohedral cells. A cube is a special case of a rhombohedron with all sides square.
In geometry, a trigonal trapezohedron is a rhombohedron in which, additionally, all six faces are congruent. Alternative names for the same shape are the trigonal deltohedron or isohedral rhombohedron. Some sources just call them rhombohedra.
A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals. It is represented by the Schläfli symbol {5,3}.
A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.
In geometry, a golden rhombus is a rhombus whose diagonals are in the golden ratio:
In the mathematical field of graph theory, the Dürer graph is an undirected graph with 12 vertices and 18 edges. It is named after Albrecht Dürer, whose 1514 engraving Melencolia I includes a depiction of Dürer's solid, a convex polyhedron having the Dürer graph as its skeleton. Dürer's solid is one of only four well-covered simple convex polyhedra.
Melencolia I is a large 1514 engraving by the German Renaissance artist Albrecht Dürer. Its central subject is an enigmatic and gloomy winged female figure thought to be a personification of melancholia – melancholy. Holding her head in her hand, she stares past the busy scene in front of her. The area is strewn with symbols and tools associated with craft and carpentry, including an hourglass, weighing scales, a hand plane, a claw hammer, and a saw. Other objects relate to alchemy, geometry or numerology. Behind the figure is a structure with an embedded magic square, and a ladder leading beyond the frame. The sky contains a rainbow, a comet or planet, and a bat-like creature bearing the text that has become the print's title.
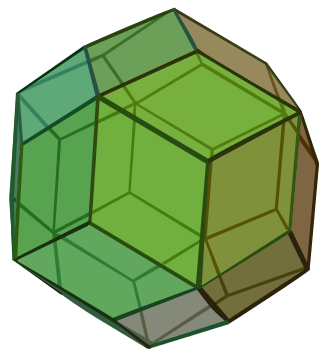
In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.
In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi) 'twenty', and ἕδρα (hédra) 'seat'. The plural can be either "icosahedra" or "icosahedrons".
{{citation}}: CS1 maint: location missing publisher (link). As cited by Weitzel (2004).{{citation}}: CS1 maint: location missing publisher (link). As cited by Lynch (1982).{{citation}}: CS1 maint: location missing publisher (link). As cited by Weitzel (2004).