In statistics, the likelihood function measures the goodness of fit of a statistical model to a sample of data for given values of the unknown parameters. It is formed from the joint probability distribution of the sample, but viewed and used as a function of the parameters only, thus treating the random variables as fixed at the observed values.

In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.
In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. The terms "distribution" and "family" are often used loosely: properly, an exponential family is a set of distributions, where the specific distribution varies with the parameter; however, a parametric family of distributions is often referred to as "a distribution", and the set of all exponential families is sometimes loosely referred to as "the" exponential family.

In probability and statistics, the Dirichlet distribution, often denoted , is a family of continuous multivariate probability distributions parameterized by a vector of positive reals. It is a multivariate generalization of the beta distribution, hence its alternative name of multivariate beta distribution (MBD). Dirichlet distributions are commonly used as prior distributions in Bayesian statistics, and in fact the Dirichlet distribution is the conjugate prior of the categorical distribution and multinomial distribution.
In statistics and information theory, a maximum entropy probability distribution has entropy that is at least as great as that of all other members of a specified class of probability distributions. According to the principle of maximum entropy, if nothing is known about a distribution except that it belongs to a certain class, then the distribution with the largest entropy should be chosen as the least-informative default. The motivation is twofold: first, maximizing entropy minimizes the amount of prior information built into the distribution; second, many physical systems tend to move towards maximal entropy configurations over time.
In probability theory the hypoexponential distribution or the generalized Erlang distribution is a continuous distribution, that has found use in the same fields as the Erlang distribution, such as queueing theory, teletraffic engineering and more generally in stochastic processes. It is called the hypoexponetial distribution as it has a coefficient of variation less than one, compared to the hyper-exponential distribution which has coefficient of variation greater than one and the exponential distribution which has coefficient of variation of one.
In statistics, a parametric model or parametric family or finite-dimensional model is a particular class of statistical models. Specifically, a parametric model is a family of probability distributions that has a finite number of parameters.
Covariance matrix adaptation evolution strategy (CMA-ES) is a particular kind of strategy for numerical optimization. Evolution strategies (ES) are stochastic, derivative-free methods for numerical optimization of non-linear or non-convex continuous optimization problems. They belong to the class of evolutionary algorithms and evolutionary computation. An evolutionary algorithm is broadly based on the principle of biological evolution, namely the repeated interplay of variation and selection: in each generation (iteration) new individuals are generated by variation, usually in a stochastic way, of the current parental individuals. Then, some individuals are selected to become the parents in the next generation based on their fitness or objective function value . Like this, over the generation sequence, individuals with better and better -values are generated.
In probability and statistics, a natural exponential family (NEF) is a class of probability distributions that is a special case of an exponential family (EF).
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.
Linear Programming Boosting (LPBoost) is a supervised classifier from the boosting family of classifiers. LPBoost maximizes a margin between training samples of different classes and hence also belongs to the class of margin-maximizing supervised classification algorithms. Consider a classification function
In probability and statistics, the class of exponential dispersion models (EDM) is a set of probability distributions that represents a generalisation of the natural exponential family. Exponential dispersion models play an important role in statistical theory, in particular in generalized linear models because they have a special structure which enables deductions to be made about appropriate statistical inference.
Although the term well-behaved statistic often seems to be used in the scientific literature in somewhat the same way as is well-behaved in mathematics it can also be assigned precise mathematical meaning, and in more than one way. In the former case, the meaning of this term will vary from context to context. In the latter case, the mathematical conditions can be used to derive classes of combinations of distributions with statistics which are well-behaved in each sense.
Starting with a sample observed from a random variable X having a given distribution law with a set of non fixed parameters which we denote with a vector , a parametric inference problem consists of computing suitable values – call them estimates – of these parameters precisely on the basis of the sample. An estimate is suitable if replacing it with the unknown parameter does not cause major damage in next computations. In Algorithmic inference, suitability of an estimate reads in terms of compatibility with the observed sample.

In probability theory and statistics, the Poisson distribution, named after French mathematician Siméon Denis Poisson, is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. The Poisson distribution can also be used for the number of events in other specified intervals such as distance, area or volume.

In probability theory and directional statistics, a wrapped exponential distribution is a wrapped probability distribution that results from the "wrapping" of the exponential distribution around the unit circle.
Natural evolution strategies (NES) are a family of numerical optimization algorithms for black box problems. Similar in spirit to evolution strategies, they iteratively update the (continuous) parameters of a search distribution by following the natural gradient towards higher expected fitness.
For certain applications in linear algebra, it is useful to know properties of the probability distribution of the largest eigenvalue of a finite sum of random matrices. Suppose is a finite sequence of random matrices. Analogous to the well-known Chernoff bound for sums of scalars, a bound on the following is sought for a given parameter t:
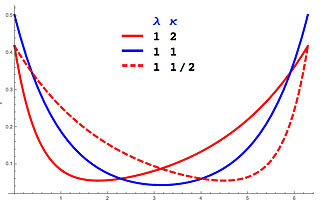
In probability theory and directional statistics, a wrapped asymmetric Laplace distribution is a wrapped probability distribution that results from the "wrapping" of the asymmetric Laplace distribution around the unit circle. For the symmetric case, the distribution becomes a wrapped Laplace distribution. The distribution of the ratio of two circular variates (Z) from two different wrapped exponential distributions will have a wrapped asymmetric Laplace distribution. These distributions find application in stochastic modelling of financial data.
In Monte Carlo Estimation, exponential tilting (ET), exponential twisting, or exponential change of measure (ECM) is a distribution shifting technique commonly used in rare-event simulation, and rejection and importance sampling in particular. Exponential tilting is also used in Esscher tilting, an indirect Edgeworth approximation technique. The earliest formalization of ECM is often attributed to Esscher with its use in importance sampling being attributed to David Siegmund. ET is known as the Esscher transform in mathematical finance and is used in such contexts as insurance futures pricing.





















































