In graph theory, a subfield of mathematics, a well-colored graph is an undirected graph for which greedy coloring uses the same number of colors regardless of the order in which colors are chosen for its vertices. That is, for these graphs, the chromatic number (minimum number of colors) and Grundy number (maximum number of greedily-chosen colors) are equal. [1]
The well-colored graphs include the complete graphs and odd-length cycle graphs (the graphs that form the exceptional cases to Brooks' theorem) as well as the complete bipartite graphs and complete multipartite graphs.
The simplest example of a graph that is not well-colored is a four-vertex path. Coloring the vertices in path order uses two colors, the optimum for this graph. However, coloring the ends of the path first (using the same color for each end) causes the greedy coloring algorithm to use three colors for this graph. Because there exists a non-optimal vertex ordering, the path is not well-colored. [2] [3]
A graph is well-colored if and only if does not have two vertex orderings for which the greedy coloring algorithm produces different numbers of colors. Therefore, recognizing non-well-colored graphs can be performed within the complexity class NP. On the other hand, a graph has Grundy number or more if and only if the graph obtained from by adding a -vertex clique is well-colored. Therefore, by a reduction from the Grundy number problem, it is NP-complete to test whether these two orderings exist. It follows that it is co-NP-complete to test whether a given graph is well-colored. [1]
A graph is hereditarily well-colored if every induced subgraph is well-colored. The hereditarily well-colored graphs are exactly the cographs, the graphs that do not have a four-vertex path as an induced subgraph. [4]
This is a glossary of graph theory terms. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by edges.
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph. Equivalently stated in symbolic terms an arbitrary graph is perfect if and only if we have:
In graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
In graph theory, an exact coloring is a (proper) vertex coloring in which every pair of colors appears on exactly one pair of adjacent vertices. That is, it is a partition of the vertices of the graph into disjoint independent sets such that, for each pair of distinct independent sets in the partition, there is exactly one edge with endpoints in each set.
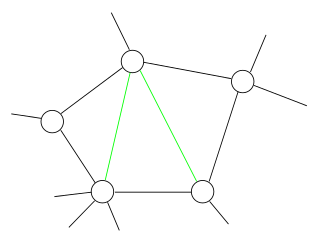
In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.
In graph theory, a circle graph is the intersection graph of a set of chords of a circle. That is, it is an undirected graph whose vertices can be associated with chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.
In graph theory, the Hadwiger conjecture states that if G is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.
In graph theory, the Grundy number or Grundy chromatic number of an undirected graph is the maximum number of colors that can be used by a greedy coloring strategy that considers the vertices of the graph in sequence and assigns each vertex its first available color, using a vertex ordering chosen to use as many colors as possible. Grundy numbers are named after P. M. Grundy, who studied an analogous concept for directed graphs in 1939. The undirected version was introduced by Christen & Selkow (1979).
In graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and each edge represents a legal move from one square to another. The same graphs can be defined mathematically as the Cartesian products of two complete graphs or as the line graphs of complete bipartite graphs.
In graph-theoretic mathematics, a star coloring of a graph G is a (proper) vertex coloring in which every path on four vertices uses at least three distinct colors. Equivalently, in a star coloring, the induced subgraphs formed by the vertices of any two colors has connected components that are star graphs. Star coloring has been introduced by Grünbaum (1973). The star chromatic number of G is the least number of colors needed to star color G.
In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not in general use the minimum number of colors possible.
In graph theory, a perfectly orderable graph is a graph whose vertices can be ordered in such a way that a greedy coloring algorithm with that ordering optimally colors every induced subgraph of the given graph. Perfectly orderable graphs form a special case of the perfect graphs, and they include the chordal graphs, comparability graphs, and distance-hereditary graphs. However, testing whether a graph is perfectly orderable is NP-complete.
In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that
In graph theory, the De Bruijn–Erdős theorem relates graph coloring of an infinite graph to the same problem on its finite subgraphs. It states that, when all finite subgraphs can be colored with colors, the same is true for the whole graph. The theorem was proved by Nicolaas Govert de Bruijn and Paul Erdős (1951), after whom it is named.
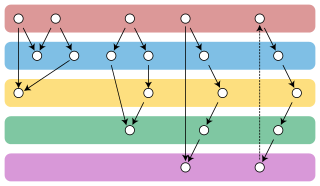
In graph theory, the Gallai–Hasse–Roy–Vitaver theorem is a form of duality between the colorings of the vertices of a given undirected graph and the orientations of its edges. It states that the minimum number of colors needed to properly color any graph G equals one plus the length of a longest path in an orientation of G chosen to minimize this path's length. The orientations for which the longest path has minimum length always include at least one acyclic orientation.
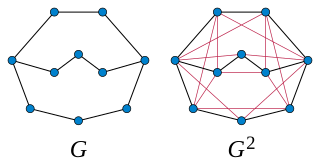
In graph theory, a branch of mathematics, the kth powerGk of an undirected graph G is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k. Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: G2 is called the square of G, G3 is called the cube of G, etc.
In graph theory, a branch of mathematics, an indifference graph is an undirected graph constructed by assigning a real number to each vertex and connecting two vertices by an edge when their numbers are within one unit of each other. Indifference graphs are also the intersection graphs of sets of unit intervals, or of properly nested intervals. Based on these two types of interval representations, these graphs are also called unit interval graphs or proper interval graphs; they form a subclass of the interval graphs.
In graph theory, coloring generally implies assignment of labels to vertices, edges or faces in a graph. The incidence coloring is a special graph labeling where in each incidence of an edge with a vertex is assigned a color under certain constraints.
