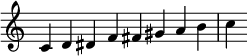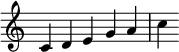In music theory, a scale is any set of musical notes ordered by fundamental frequency or pitch. A scale ordered by increasing pitch is an ascending scale, and a scale ordered by decreasing pitch is a descending scale.

Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2. This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2, which is ≈ 702 cents wide.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.
In music theory, the tritone is defined as a musical interval spanning three adjacent whole tones. For instance, the interval from F up to the B above it is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B.
An altered chord is a chord that replaces one or more notes from the diatonic scale with a neighboring pitch from the chromatic scale. By the broadest definition, any chord with a non-diatonic chord tone is an altered chord. The simplest example of altered chords is the use of borrowed chords, chords borrowed from the parallel key, and the most common is the use of secondary dominants. As Alfred Blatter explains, "An altered chord occurs when one of the standard, functional chords is given another quality by the modification of one or more components of the chord."
An octatonic scale is any eight-note musical scale. However, the term most often refers to the ancohemitonic symmetric scale composed of alternating whole and half steps, as shown at right. In classical theory, this symmetrical scale is commonly called the octatonic scale, although there are a total of 43 enharmonically inequivalent, transpositionally inequivalent eight-note sets.
A jazz scale is any musical scale used in jazz. Many "jazz scales" are common scales drawn from Western European classical music, including the diatonic, whole-tone, octatonic, and the modes of the ascending melodic minor. All of these scales were commonly used by late nineteenth and early twentieth-century composers such as Rimsky-Korsakov, Debussy, Ravel and Stravinsky, often in ways that directly anticipate jazz practice. Some jazz scales, such as the bebop scales, add additional chromatic passing tones to the familiar diatonic scales.

In music, a chord is a group of two or more notes played simultaneously, typically consisting of a root note, a third, and a fifth. Chords are the building blocks of harmony and form the harmonic foundation of a piece of music. They can be major, minor, diminished, augmented, or extended, depending on the intervals between the notes and their arrangement. Chords provide the harmonic support and coloration that accompany melodies and contribute to the overall sound and mood of a musical composition. For many practical and theoretical purposes, arpeggios and other types of broken chords may also be considered as chords in the right musical context.
In music theory, an augmented sixth chord contains the interval of an augmented sixth, usually above its bass tone. This chord has its origins in the Renaissance, was further developed in the Baroque, and became a distinctive part of the musical style of the Classical and Romantic periods.
In music, a triad is a set of three notes that can be stacked vertically in thirds. Triads are the most common chords in Western music.

A heptatonic scale is a musical scale that has seven pitches, or tones, per octave. Examples include:
Jazz chords are chords, chord voicings and chord symbols that jazz musicians commonly use in composition, improvisation, and harmony. In jazz chords and theory, most triads that appear in lead sheets or fake books can have sevenths added to them, using the performer's discretion and ear. For example, if a tune is in the key of C, if there is a G chord, the chord-playing performer usually voices this chord as G7. While the notes of a G7 chord are G–B–D–F, jazz often omits the fifth of the chord—and even the root if playing in a group. However, not all jazz pianists leave out the root when they play voicings: Bud Powell, one of the best-known of the bebop pianists, and Horace Silver, whose quintet included many of jazz's biggest names from the 1950s to the 1970s, included the root note in their voicings.
The Petrushka chord is a recurring polytonal device used in Igor Stravinsky's ballet Petrushka and in later music. These two major triads, C major and F♯ major – a tritone apart – clash, "horribly with each other", when sounded together and create a dissonant chord.

In musical set theory, an interval vector is an array of natural numbers which summarize the intervals present in a set of pitch classes. Other names include: ic vector, PIC vector and APIC vector
In music, harmonization is the chordal accompaniment to a line or melody: "Using chords and melodies together, making harmony by stacking scale tones as triads".
Post-tonal music theory is the set of theories put forward to describe music written outside of, or 'after', the tonal system of the common practice period. It revolves around the idea of 'emancipating dissonance', that is, freeing the structure of music from the familiar harmonic patterns that are derived from natural overtones. As music becomes more complex, dissonance becomes indistinguishable from consonance.
A chordioid, also called chord fragment or fragmentary voicing or partial voicing, is a group of musical notes which does not qualify as a chord under a given chord theory, but still useful to name and reify for other reasons.
The Hungarian major scale is a heptatonic scale subset of the octatonic scale with an omitted ♭2 degree. It has the following interval structure in semitones: 3, 1, 2, 1, 2, 1, 2, giving it the notes C D♯ E F♯ G A B♭ in the key of C. It is, "used extensively in Hungarian gypsy music [sic]", as well as in classical music by composers including Franz Liszt and Zoltán Kodály ," as well as in Thea Musgrave's Horn Concerto (1971). As a chord scale, Hungarian Major is both a dominant and a diminished scale, with a fully diminished seventh chord composed of C, D#, F#, and A, and a dominant seventh chord composed of C, E, G, and Bb. This is an enharmonic mode of Bb Harmonic Major, along with G Harmonic Minor and E Hungarian Minor. The root note of D Aeolian Dominant is raised a semitone to D#, and the root note of B Phrygian Dominant lowered a semitone to Bb. There is also a ♮6 & ♮2 with the Bb Super Lydian Augmented scale, lowering the C# & G# to C♮ & G♮.
A decatonic scale is a ten note musical scale. If the notes are ordered, a decatonic set has 3,628,800 permutations, however, in twelve tone equal temperament only six unordered ten note sets exist, 10-1—10-6:
The Romanian major scale is a heptatonic scale subset of the octatonic scale with an omitted ♭3 degree. It is noted for its flattened 2nd and sharpened fourth degrees, the latter a distinctive feature of Romanian traditional music. It has the following interval structure in semitones: 1, 3, 2, 1, 2, 1, 2, giving it the notes C, D♭, E, F♯, G, A, B♭ in the key of C. Though it is called a major scale, it is typically played over a C13 dominant chord. This is an enharmonic mode of B Harmonic Minor, along with D Harmonic Major. The root note of F Harmonic Major is raised a semitone to F#, and the root note of D Aeolian Dominant lowered a semitone to Db. There is also a ♮6 with the Db Super Lydian Augmented scale, lowering the B♮ to Bb.