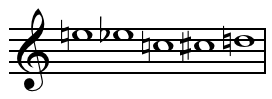In music theory, a scale is "any consecutive series of notes that form a progression between one note and its octave", typically by order of pitch or fundamental frequency.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.
An octatonic scale is any eight-note musical scale. However, the term most often refers to the ancohemitonic symmetric scale composed of alternating whole and half steps, as shown at right. In classical theory, this symmetrical scale is commonly called the octatonic scale, although there are a total of 43 enharmonically inequivalent, transpositionally inequivalent eight-note sets.

Musical set theory provides concepts for categorizing musical objects and describing their relationships. Howard Hanson first elaborated many of the concepts for analyzing tonal music. Other theorists, such as Allen Forte, further developed the theory for analyzing atonal music, drawing on the twelve-tone theory of Milton Babbitt. The concepts of musical set theory are very general and can be applied to tonal and atonal styles in any equal temperament tuning system, and to some extent more generally than that.
In music, a hexachord is a six-note series, as exhibited in a scale or tone row. The term was adopted in this sense during the Middle Ages and adapted in the 20th century in Milton Babbitt's serial theory. The word is taken from the Greek: ἑξάχορδος, compounded from ἕξ and χορδή, and was also the term used in music theory up to the 18th century for the interval of a sixth.
In music using the twelve tone technique, combinatoriality is a quality shared by twelve-tone tone rows whereby each section of a row and a proportionate number of its transformations combine to form aggregates. Much as the pitches of an aggregate created by a tone row do not need to occur simultaneously, the pitches of a combinatorially created aggregate need not occur simultaneously. Arnold Schoenberg, creator of the twelve-tone technique, often combined P-0/I-5 to create "two aggregates, between the first hexachords of each, and the second hexachords of each, respectively."

In music theory, complement refers to either traditional interval complementation, or the aggregate complementation of twelve-tone and serialism.
In music, transposition refers to the process or operation of moving a collection of notes up or down in pitch by a constant interval.
The shifting of a melody, a harmonic progression or an entire musical piece to another key, while maintaining the same tone structure, i.e. the same succession of whole tones and semitones and remaining melodic intervals.

The mathematical operations of multiplication have several applications to music. Other than its application to the frequency ratios of intervals, it has been used in other ways for twelve-tone technique, and musical set theory. Additionally ring modulation is an electrical audio process involving multiplication that has been used for musical effect.
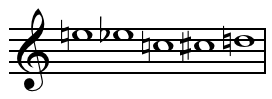
A set in music theory, as in mathematics and general parlance, is a collection of objects. In musical contexts the term is traditionally applied most often to collections of pitches or pitch-classes, but theorists have extended its use to other types of musical entities, so that one may speak of sets of durations or timbres, for example.
David Benjamin Lewin was an American music theorist, music critic and composer. Called "the most original and far-ranging theorist of his generation", he did his most influential theoretical work on the development of transformational theory, which involves the application of mathematical group theory to music.
An all-interval tetrachord is a tetrachord, a collection of four pitch classes, containing all six interval classes. There are only two possible all-interval tetrachords, when expressed in prime form. In set theory notation, these are [0,1,4,6] (4-Z15) and [0,1,3,7] (4-Z29). Their inversions are [0,2,5,6] (4-Z15b) and [0,4,6,7] (4-Z29b). The interval vector for all all-interval tetrachords is [1,1,1,1,1,1].
In music theory, an inversion is a rearrangement of the top-to-bottom elements in an interval, a chord, a melody, or a group of contrapuntal lines of music. In each of these cases, "inversion" has a distinct but related meaning. The concept of inversion also plays an important role in musical set theory.

Neo-Riemannian theory is a loose collection of ideas present in the writings of music theorists such as David Lewin, Brian Hyer, Richard Cohn, and Henry Klumpenhouwer. What binds these ideas is a central commitment to relating harmonies directly to each other, without necessary reference to a tonic. Initially, those harmonies were major and minor triads; subsequently, neo-Riemannian theory was extended to standard dissonant sonorities as well. Harmonic proximity is characteristically gauged by efficiency of voice leading. Thus, C major and E minor triads are close by virtue of requiring only a single semitonal shift to move from one to the other. Motion between proximate harmonies is described by simple transformations. For example, motion between a C major and E minor triad, in either direction, is executed by an "L" transformation. Extended progressions of harmonies are characteristically displayed on a geometric plane, or map, which portrays the entire system of harmonic relations. Where consensus is lacking is on the question of what is most central to the theory: smooth voice leading, transformations, or the system of relations that is mapped by the geometries. The theory is often invoked when analyzing harmonic practices within the Late Romantic period characterized by a high degree of chromaticism, including work of Schubert, Liszt, Wagner and Bruckner.

In musical set theory, a Forte number is the pair of numbers Allen Forte assigned to the prime form of each pitch class set of three or more members in The Structure of Atonal Music. The first number indicates the number of pitch classes in the pitch class set and the second number indicates the set's sequence in Forte's ordering of all pitch class sets containing that number of pitches.
In music, the "Ode-to-Napoleon" hexachord is the hexachord named after its use in the twelve-tone piece Ode to Napoleon Buonaparte Op. 41 (1942) by Arnold Schoenberg. Containing the pitch-classes 014589 it is given Forte number 6–20 in Allen Forte's taxonomic system. The primary form of the tone row used in the Ode allows the triads of G minor, E♭ minor, and B minor to easily appear.
6-Z44 (012569), known as the Schoenberg hexachord, is Arnold Schoenberg's signature hexachord, as one transposition contains the pitches [A], Es, C, H, B, E, G, E♭, B, and B♭ being Es, H, and B in German.

In music, a similarity relation or pitch-class similarity is a comparison between sets of the same cardinality, based upon shared pitch class and/or interval class content.
Musicology commonly classifies scales as either hemitonic or anhemitonic. Hemitonic scales contain one or more semitones, while anhemitonic scales do not contain semitones. For example, in traditional Japanese music, the anhemitonic yo scale is contrasted with the hemitonic in scale. The simplest and most commonly used scale in the world is the atritonic anhemitonic "major" pentatonic scale. The whole tone scale is also anhemitonic.