In music theory, a diatonic scale is any heptatonic scale that includes five whole steps and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, depending on their position in the scale. This pattern ensures that, in a diatonic scale spanning more than one octave, all the half steps are maximally separated from each other.

Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2. This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2, which is ≈ 702 cents wide.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.

The chromatic scale is a set of twelve pitches used in tonal music, with notes separated by the interval of a semitone. Chromatic instruments, such as the piano, are made to produce the chromatic scale, while other instruments capable of continuously variable pitch, such as the trombone and violin, can also produce microtones, or notes between those available on a piano.
In music theory, the tritone is defined as a musical interval spanning three adjacent whole tones. For instance, the interval from F up to the B above it is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B.
In music theory, a tetrachord is a series of four notes separated by three intervals. In traditional music theory, a tetrachord always spanned the interval of a perfect fourth, a 4:3 frequency proportion —but in modern use it means any four-note segment of a scale or tone row, not necessarily related to a particular tuning system.

In music theory, the circle of fifths is a way of organizing pitches as a sequence of perfect fifths. Starting on a C, and using the standard system of tuning for Western music, the sequence is: C, G, D, A, E, B, F♯, C♯, G♯, D♯, A♯, E♯ (F), C. This order places the most closely related key signatures adjacent to one another. It is usually illustrated in the form of a circle.

A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale, visually seen on a keyboard as the distance between two keys that are adjacent to each other. For example, C is adjacent to C♯; the interval between them is a semitone.
In music, a triad is a set of three notes that can be stacked vertically in thirds. Triads are the most common chords in Western music.
In the musical system of ancient Greece, genus is a term used to describe certain classes of intonations of the two movable notes within a tetrachord. The tetrachordal system was inherited by the Latin medieval theory of scales and by the modal theory of Byzantine music; it may have been one source of the later theory of the jins of Arabic music. In addition, Aristoxenus calls some patterns of rhythm "genera".

The musical operation of scalar transposition shifts every note in a melody by the same number of scale steps. The musical operation of chromatic transposition shifts every note in a melody by the same distance in pitch class space. In general, for a given scale S, the scalar transpositions of a line L can be grouped into categories, or transpositional set classes, whose members are related by chromatic transposition. In diatonic set theory cardinality equals variety when, for any melodic line L in a particular scale S, the number of these classes is equal to the number of distinct pitch classes in the line L.
In diatonic set theory structure implies multiplicity is a quality of a collection or scale. For collections or scales which have this property, the interval series formed by the shortest distance around a diatonic circle of fifths between members of a series indicates the number of unique interval patterns formed by diatonic transpositions of that series. Structure refers to the intervals in relation to the circle of fifths; multiplicity refers to the number of times each different (adjacent) interval pattern occurs. The property was first described by John Clough and Gerald Myerson in "Variety and Multiplicity in Diatonic Systems" (1985).
Diatonic set theory is a subdivision or application of musical set theory which applies the techniques and analysis of discrete mathematics to properties of the diatonic collection such as maximal evenness, Myhill's property, well formedness, the deep scale property, cardinality equals variety, and structure implies multiplicity. The name is something of a misnomer as the concepts involved usually apply much more generally, to any periodically repeating scale.

In scale (music) theory, a maximally even set (scale) is one in which every generic interval has either one or two consecutive integers specific intervals-in other words a scale whose notes (pcs) are "spread out as much as possible." This property was first described by John Clough and Jack Douthett. Clough and Douthett also introduced the maximally even algorithm. For a chromatic cardinality c and pc-set cardinality d a maximally even set is

In diatonic set theory a generic interval is the number of scale steps between notes of a collection or scale. The largest generic interval is one less than the number of scale members.

In diatonic set theory, a bisector divides the octave approximately in half and may be used in place of a generator to derive collections for which structure implies multiplicity is not true such as the ascending melodic minor, harmonic minor, and octatonic scales. Well formed generated collections generators and bisectors coincide, such as the perfect fifth in the diatonic collection. The term was introduced by Jay Rahn (1977), who considers any division between one and two thirds as approximately half and who applied the term only the equally spaced collections. Clough and Johnson both adapt the term to apply to generic scale steps. Rahn also uses aliquant bisector for bisectors which may be used to generate every note in a collection, in which case the bisector and the number of notes must be coprime. Bisectors may be used to produce the diatonic, harmonic minor, and ascending melodic minor collections.
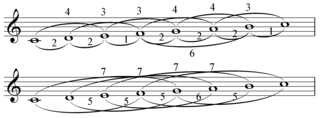
In diatonic set theory, Rothenberg propriety is an important concept, lack of contradiction and ambiguity, in the general theory of musical scales which was introduced by David Rothenberg in a seminal series of papers in 1978. The concept was independently discovered in a more restricted context by Gerald Balzano, who termed it coherence.

Diatonic and chromatic are terms in music theory that are used to characterize scales. The terms are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900.
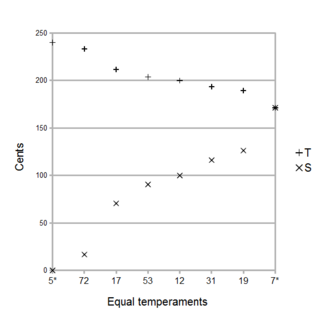
A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's. In such a tuning, then the notes are connected together in a chain of seven fifths, all the same size which makes it a Linear temperament with the tempered fifth as a generator.

In music, a common tone is a pitch class that is a member of, or common to two or more scales or sets.












