In music theory, a diatonic scale is any heptatonic scale that includes five whole steps and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, depending on their position in the scale. This pattern ensures that, in a diatonic scale spanning more than one octave, all the half steps are maximally separated from each other.
In music theory, a scale is any set of musical notes ordered by fundamental frequency or pitch. A scale ordered by increasing pitch is an ascending scale, and a scale ordered by decreasing pitch is a descending scale.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.
In music theory, the key of a piece is the group of pitches, or scale, that forms the basis of a musical composition in Western classical music, art music, and pop music.
Tonality or key: Music which uses the notes of a particular scale is said to be "in the key of" that scale or in the tonality of that scale.
An octatonic scale is any eight-note musical scale. However, the term most often refers to the symmetric scale composed of alternating whole and half steps, as shown at right. In classical theory, this symmetrical scale is commonly called the octatonic scale, although there are a total of 42 enharmonically non-equivalent, transpositionally non-equivalent eight-note sets.

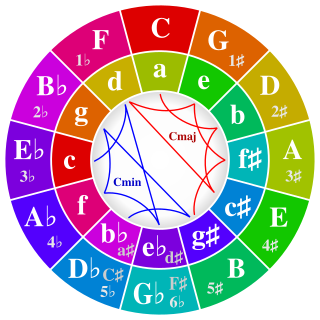
In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths.. If C is chosen as a starting point, the sequence is: C, G, D, A, E, B, F♯, C♯, A♭, E♭, B♭, F. Continuing the pattern from F returns the sequence to its starting point of C. This order places the most closely related key signatures adjacent to one another. It is usually illustrated in the form of a circle.
In music, transposition refers to the process or operation of moving a collection of notes up or down in pitch by a constant interval.
The shifting of a melody, a harmonic progression or an entire musical piece to another key, while maintaining the same tone structure, i.e. the same succession of whole tones and semitones and remaining melodic intervals.

The musical operation of scalar transposition shifts every note in a melody by the same number of scale steps. The musical operation of chromatic transposition shifts every note in a melody by the same distance in pitch class space. In general, for a given scale S, the scalar transpositions of a line L can be grouped into categories, or transpositional set classes, whose members are related by chromatic transposition. In diatonic set theory cardinality equals variety when, for any melodic line L in a particular scale S, the number of these classes is equal to the number of distinct pitch classes in the line L.
In diatonic set theory, a generated collection is a collection or scale formed by repeatedly adding a constant interval in integer notation, the generator, also known as an interval cycle, around the chromatic circle until a complete collection or scale is formed. All scales with the deep scale property can be generated by any interval coprime with twelve.
Diatonic set theory is a subdivision or application of musical set theory which applies the techniques and analysis of discrete mathematics to properties of the diatonic collection such as maximal evenness, Myhill's property, well formedness, the deep scale property, cardinality equals variety, and structure implies multiplicity. The name is something of a misnomer as the concepts involved usually apply much more generally, to any periodically repeating scale.

In scale (music) theory, a maximally even set (scale) is one in which every generic interval has either one or two consecutive integers specific intervals-in other words a scale whose notes (pcs) are "spread out as much as possible." This property was first described by John Clough and Jack Douthett. Clough and Douthett also introduced the maximally even algorithm. For a chromatic cardinality c and pc-set cardinality d a maximally even set is

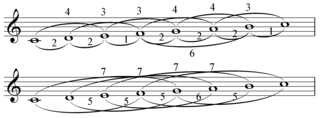
In diatonic set theory a generic interval is the number of scale steps between notes of a collection or scale. The largest generic interval is one less than the number of scale members.
The Hypophrygian mode, literally meaning "below Phrygian ", is a musical mode or diatonic scale in medieval chant theory, the fourth mode of church music. This mode is the plagal counterpart of the authentic third mode, which was called Phrygian. In the Middle Ages and Renaissance this mode was described in two ways: the diatonic scale from B to B an octave above, divided at the mode final E ; and as a mode with final E and ambitus from the A below to the C above. The note A above the final had an important melodic function. The melodic range of the ecclesiastical Hypophrygian mode therefore goes from the perfect fourth or fifth below the tonic to the perfect fifth or minor sixth above.

In music theory, the harmonic major scale is a musical scale found in some music from the common practice era and now used occasionally, most often in jazz. In George Russell's Lydian Chromatic Concept it is the fifth mode (V) of the Lydian Diminished scale. It corresponds to the Raga Sarasangi in Indian Carnatic music.

In diatonic set theory, a bisector divides the octave approximately in half and may be used in place of a generator to derive collections for which structure implies multiplicity is not true such as the ascending melodic minor, harmonic minor, and octatonic scales. Well formed generated collections generators and bisectors coincide, such as the perfect fifth in the diatonic collection. The term was introduced by Jay Rahn (1977), who considers any division between one and two thirds as approximately half and who applied the term only the equally spaced collections. Clough and Johnson both adapt the term to apply to generic scale steps. Rahn also uses aliquant bisector for bisectors which may be used to generate every note in a collection, in which case the bisector and the number of notes must be coprime. Bisectors may be used to produce the diatonic, harmonic minor, and ascending melodic minor collections.
In music, a sequence is the restatement of a motif or longer melodic passage at a higher or lower pitch in the same voice. It is one of the most common and simple methods of elaborating a melody in eighteenth and nineteenth century classical music. Characteristics of sequences:
In diatonic set theory, Rothenberg propriety is an important concept, lack of contradiction and ambiguity, in the general theory of musical scales which was introduced by David Rothenberg in a seminal series of papers in 1978. The concept was independently discovered in a more restricted context by Gerald Balzano, who termed it coherence.

Diatonic and chromatic are terms in music theory that are most often used to characterize scales, and are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900.
In music, a symmetric scale is a music scale which equally divides the octave. The concept and term appears to have been introduced by Joseph Schillinger and further developed by Nicolas Slonimsky as part of his famous Thesaurus of Scales and Melodic Patterns. In twelve-tone equal temperament, the octave can only be equally divided into two, three, four, six, or twelve parts, which consequently may be filled in by adding the same exact interval or sequence of intervals to each resulting note.

In music, a common tone is a pitch class that is a member of, or common to two or more scales or sets.










