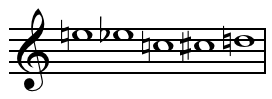In music theory, a scale is "any consecutive series of notes that form a progression between one note and its octave", typically by order of pitch or fundamental frequency.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.
An octatonic scale is any eight-note musical scale. However, the term most often refers to the ancohemitonic symmetric scale composed of alternating whole and half steps, as shown at right. In classical theory, this symmetrical scale is commonly called the octatonic scale, although there are a total of 43 enharmonically inequivalent, transpositionally inequivalent eight-note sets.
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave position." Important to musical set theory, a pitch class is "all pitches related to each other by octave, enharmonic equivalence, or both." Thus, using scientific pitch notation, the pitch class "C" is the set

Musical set theory provides concepts for categorizing musical objects and describing their relationships. Howard Hanson first elaborated many of the concepts for analyzing tonal music. Other theorists, such as Allen Forte, further developed the theory for analyzing atonal music, drawing on the twelve-tone theory of Milton Babbitt. The concepts of musical set theory are very general and can be applied to tonal and atonal styles in any equal temperament tuning system, and to some extent more generally than that.

In music theory, complement refers to either traditional interval complementation, or the aggregate complementation of twelve-tone and serialism.

In music, a permutation (order) of a set is any ordering of the elements of that set. A specific arrangement of a set of discrete entities, or parameters, such as pitch, dynamics, or timbre. Different permutations may be related by transformation, through the application of zero or more operations, such as transposition, inversion, retrogradation, circular permutation, or multiplicative operations. These may produce reorderings of the members of the set, or may simply map the set onto itself.
In music, transposition refers to the process or operation of moving a collection of notes up or down in pitch by a constant interval.
The shifting of a melody, a harmonic progression or an entire musical piece to another key, while maintaining the same tone structure, i.e. the same succession of whole tones and semitones and remaining melodic intervals.

In music, an interval cycle is a collection of pitch classes created from a sequence of the same interval class. In other words, a collection of pitches by starting with a certain note and going up by a certain interval until the original note is reached. In other words, interval cycles "unfold a single recurrent interval in a series that closes with a return to the initial pitch class". See: wikt:cycle.

The mathematical operations of multiplication have several applications to music. Other than its application to the frequency ratios of intervals, it has been used in other ways for twelve-tone technique, and musical set theory. Additionally ring modulation is an electrical audio process involving multiplication that has been used for musical effect.
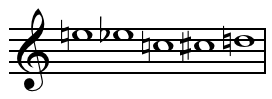
A set in music theory, as in mathematics and general parlance, is a collection of objects. In musical contexts the term is traditionally applied most often to collections of pitches or pitch-classes, but theorists have extended its use to other types of musical entities, so that one may speak of sets of durations or timbres, for example.

In musical set theory, an interval vector is an array of natural numbers which summarize the intervals present in a set of pitch classes. Other names include: ic vector, PIC vector and APIC vector
In music theory, an inversion is a rearrangement of the top-to-bottom elements in an interval, a chord, a melody, or a group of contrapuntal lines of music. In each of these cases, "inversion" has a distinct but related meaning. The concept of inversion also plays an important role in musical set theory.
Fritz Heinrich Klein was an Austrian composer.
Post-tonal music theory is the set of theories put forward to describe music written outside of, or 'after', the tonal system of the common practice period. It revolves around the idea of 'emancipating dissonance', that is, freeing the structure of music from the familiar harmonic patterns that are derived from natural overtones. As music becomes more complex, dissonance becomes indistinguishable from consonance.

In music, a Klumpenhouwer Network is "any network that uses T and/or I operations to interpret interrelations among pcs". According to George Perle, "a Klumpenhouwer network is a chord analyzed in terms of its dyadic sums and differences," and "this kind of analysis of triadic combinations was implicit in," his "concept of the cyclic set from the beginning", cyclic sets being those "sets whose alternate elements unfold complementary cycles of a single interval." It is named for the Canadian music theorist Henry Klumpenhouwer, a former doctoral student of David Lewin's.

In music, an all-interval twelve-tone row, series, or chord, is a twelve-tone tone row arranged so that it contains one instance of each interval within the octave, 1 through 11. A "twelve-note spatial set made up of the eleven intervals [between consecutive pitches]." There are 1,928 distinct all-interval twelve-tone rows. These sets may be ordered in time or in register. "Distinct" in this context means in transpositionally and rotationally normal form, and disregarding inversionally related forms. These 1,928 tone rows have been independently rediscovered several times, their first computation probably was by Andre Riotte in 1961.

In musical set theory, there are four kinds of interval:
John Rahn, born on February 26, 1944, in New York City, is a music theorist, composer, bassoonist, and Professor of Music at the University of Washington School of Music, Seattle. A former student of Milton Babbitt and Benjamin Boretz, he was editor of Perspectives of New Music from 1983 to 1993 and since 2001 has been co-editor with Benjamin Boretz and Robert Morris.