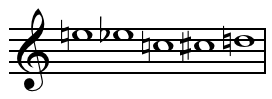Atonality in its broadest sense is music that lacks a tonal center, or key. Atonality, in this sense, usually describes compositions written from about the early 20th-century to the present day, where a hierarchy of harmonies focusing on a single, central triad is not used, and the notes of the chromatic scale function independently of one another. More narrowly, the term atonality describes music that does not conform to the system of tonal hierarchies that characterized European classical music between the seventeenth and nineteenth centuries. "The repertory of atonal music is characterized by the occurrence of pitches in novel combinations, as well as by the occurrence of familiar pitch combinations in unfamiliar environments".
In music theory, a tetrachord is a series of four notes separated by three intervals. In traditional music theory, a tetrachord always spanned the interval of a perfect fourth, a 4:3 frequency proportion —but in modern use it means any four-note segment of a scale or tone row, not necessarily related to a particular tuning system.
In the fields of databases and transaction processing, a schedule of a system is an abstract model to describe the order of executions in a set of transactions running in the system. Often it is a list of operations (actions) ordered by time, performed by a set of transactions that are executed together in the system. If the order in time between certain operations is not determined by the system, then a partial order is used. Examples of such operations are requesting a read operation, reading, writing, aborting, committing, requesting a lock, locking, etc. Often, only a subset of the transaction operation types are included in a schedule.

Musical set theory provides concepts for categorizing musical objects and describing their relationships. Howard Hanson first elaborated many of the concepts for analyzing tonal music. Other theorists, such as Allen Forte, further developed the theory for analyzing atonal music, drawing on the twelve-tone theory of Milton Babbitt. The concepts of musical set theory are very general and can be applied to tonal and atonal styles in any equal temperament tuning system, and to some extent more generally than that.

In musical set theory, an interval class, also known as unordered pitch-class interval, interval distance, undirected interval, or "(even completely incorrectly) as 'interval mod 6'", is the shortest distance in pitch class space between two unordered pitch classes. For example, the interval class between pitch classes 4 and 9 is 5 because 9 − 4 = 5 is less than 4 − 9 = −5 ≡ 7 (mod 12). See modular arithmetic for more on modulo 12. The largest interval class is 6 since any greater interval n may be reduced to 12 − n.

In music theory, complement refers to either traditional interval complementation, or the aggregate complementation of twelve-tone and serialism.
In music, transposition refers to the process or operation of moving a collection of notes up or down in pitch by a constant interval.
The shifting of a melody, a harmonic progression or an entire musical piece to another key, while maintaining the same tone structure, i.e. the same succession of whole tones and semitones and remaining melodic intervals.

Allen Forte was an American music theorist and musicologist. He was Battell Professor Emeritus of the Theory of Music at Yale University and specialized in 20th-century atonal music and music analysis.
In music theory, prolongation is the process in tonal music through which a pitch, interval, or consonant triad is considered to govern spans of music when not physically sounding. It is a central principle in the music-analytic methodology of Schenkerian analysis, conceived by Austrian theorist Heinrich Schenker. The English term usually translates Schenker's Auskomponierung. According to Fred Lerdahl, "The term 'prolongation' [...] usually means 'composing out' ."
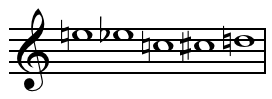
A set in music theory, as in mathematics and general parlance, is a collection of objects. In musical contexts the term is traditionally applied most often to collections of pitches or pitch-classes, but theorists have extended its use to other types of musical entities, so that one may speak of sets of durations or timbres, for example.

In musical set theory, an interval vector is an array of natural numbers which summarize the intervals present in a set of pitch classes. Other names include: ic vector, PIC vector and APIC vector
An all-interval tetrachord is a tetrachord, a collection of four pitch classes, containing all six interval classes. There are only two possible all-interval tetrachords, when expressed in prime form. In set theory notation, these are [0,1,4,6] (4-Z15) and [0,1,3,7] (4-Z29). Their inversions are [0,2,5,6] (4-Z15b) and [0,4,6,7] (4-Z29b). The interval vector for all all-interval tetrachords is [1,1,1,1,1,1].

A tetrad is a set of four notes in music theory. When these four notes form a tertian chord they are more specifically called a seventh chord, after the diatonic interval from the root of the chord to its fourth note. Four-note chords are often formed of intervals other than thirds in 20th- and 21st-century music, however, where they are more generally referred to as tetrads. Allen Forte in his The Structure of Atonal Music never uses the term "tetrad", but occasionally employs the word tetrachord to mean any collection of four pitch classes. In 20th-century music theory, such sets of four pitch classes are usually called "tetrachords".

In music, a Klumpenhouwer Network is "any network that uses T and/or I operations to interpret interrelations among pcs". According to George Perle, "a Klumpenhouwer network is a chord analyzed in terms of its dyadic sums and differences," and "this kind of analysis of triadic combinations was implicit in," his "concept of the cyclic set from the beginning", cyclic sets being those "sets whose alternate elements unfold complementary cycles of a single interval." It is named for the Canadian music theorist Henry Klumpenhouwer, a former doctoral student of David Lewin's.

In musical set theory, a Forte number is the pair of numbers Allen Forte assigned to the prime form of each pitch class set of three or more members in The Structure of Atonal Music. The first number indicates the number of pitch classes in the pitch class set and the second number indicates the set's sequence in Forte's ordering of all pitch class sets containing that number of pitches.
In music theory, equivalence class is an equality (=) or equivalence between properties of sets (unordered) or twelve-tone rows. A relation rather than an operation, it may be contrasted with derivation. "It is not surprising that music theorists have different concepts of equivalence [from each other]..." "Indeed, an informal notion of equivalence has always been part of music theory and analysis. Pitch class set theory, however, has adhered to formal definitions of equivalence." Traditionally, octave equivalency is assumed, while inversional, permutational, and transpositional equivalency may or may not be considered.
In music, the 'Farben' chord is a chord, in ascending order C–G♯–B–E–A, named after its use in Five Pieces for Orchestra, Op.16, No. 3, "Farben" by Arnold Schoenberg. Its unordered pitch-class content in normal form is 01348, its Forte number is 5-z17, in the taxonomy of Allen Forte.
In music, the "Ode-to-Napoleon" hexachord is the hexachord named after its use in the twelve-tone piece Ode to Napoleon Buonaparte Op. 41 (1942) by Arnold Schoenberg. Containing the pitch-classes 014589 it is given Forte number 6–20 in Allen Forte's taxonomic system. The primary form of the tone row used in the Ode allows the triads of G minor, E♭ minor, and B minor to easily appear.

In musical set theory, there are four kinds of interval: