
In music, a common tone is a pitch class that is a member of, or common to (shared by) two or more scales or sets.

In music, a common tone is a pitch class that is a member of, or common to (shared by) two or more scales or sets.

A common tone is a pitch class that is a member of, or common to, a musical scale and a transposition of that scale, as in modulation ( Johnson 2003 , p. 42). Six of seven possible common tones are shared by closely related keys, though keys may also be thought of as more or less closely related according to their number of common tones. "Obviously, tonal distance is in some sense a function of the extent of intersection between diatonic PC collections of tonal systems" ( Berry 1987 , p. 80).
| Diatonic transposition | 0 | 1/e | 2/t | 3/9 | 4/8 | 5/7 | 6/6 |
|---|---|---|---|---|---|---|---|
| Common tones | 7 | 2 | 5 | 4 | 3 | 6 | 1 |
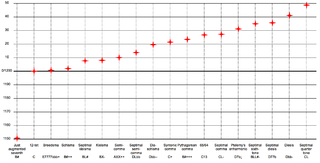
In diatonic set theory the common tone theorem explains that scales possessing the deep scale property share a different number of common tones, not counting enharmonic equivalents (for example, C♯ and C♭ have no common tones with C major), for every different transposition of the scale. However many times an interval class occurs in a diatonic scale is the number of tones common both to the original scale and a scale transposed by that particular interval class. For example, then, modulation to the dominant (transposition by a perfect fifth) includes six common tones between the keys as there are six perfect fifths in a diatonic scale, while transposition by the tritone includes only one common tone as there is only one tritone in a diatonic scale ( Johnson 2003 , p. 42).

| Key | IC | CT | Notes common with C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C | 0 | NA | C | D | E | F | G | A | B |
| B | 1 | 2 | E | B | |||||
| D♭ | C | F | |||||||
| D | 2 | 5 | D | E | G | A | B | ||
| B♭ | C | D | F | G | A | ||||
| A | 3 | 4 | D | E | A | B | |||
| E♭ | C | D | F | G | |||||
| E | 4 | 3 | E | A | B | ||||
| A♭ | C | F | G | ||||||
| G | 5 | 6 | C | D | E | G | A | B | |
| F | C | D | E | F | G | A | |||
| F♯ | 6 | 1 | B | ||||||
| G♭ | F | ||||||||



In diatonic set theory, the deep scale property is the quality of pitch class collections or scales containing each interval class a unique number of times. Examples include the diatonic scale (including major, natural minor, and the modes) ( Johnson 2003 , p. 41). In twelve-tone equal temperament, all scales with the deep scale property can be generated with any interval coprime with twelve ( Johnson 2003 , p. 83).
For example, the diatonic scale's interval vector contains:
| PC | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Occurrence | 2 | 5 | 4 | 3 | 6 | 1 |
The common tone theorem describes that scales possessing the deep scale property share a different number of common tones for every different transposition of the scale, suggesting an explanation for the use and usefulness of the diatonic collection ( Johnson 2003 , p. 42).
In contrast, the whole tone scale's interval vector contains:
| PC | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Occurrence | 0 | 6 | 0 | 6 | 0 | 3 |
and has only two distinct transpositions (every even transposition of the whole tone scale is identical with the original and every odd transposition has no common tones whatsoever).
In music theory, a diatonic scale is any heptatonic scale that includes five whole steps and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, depending on their position in the scale. This pattern ensures that, in a diatonic scale spanning more than one octave, all the half steps are maximally separated from each other.
In music theory, a scale is any set of musical notes ordered by fundamental frequency or pitch. A scale ordered by increasing pitch is an ascending scale, and a scale ordered by decreasing pitch is a descending scale.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.

The chromatic scale is a set of twelve pitches used in tonal music, with notes separated by the interval of a semitone. Almost all western musical instruments, such as the piano, are made to produce the chromatic scale, while other instruments such as the trombone and violin can also produce microtones, or notes between those available on a piano.
In music theory, the tritone is defined as a musical interval composed of three adjacent whole tones. For instance, the interval from F up to the B above it is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B. According to this definition, within a diatonic scale there is only one tritone for each octave. For instance, the above-mentioned interval F–B is the only tritone formed from the notes of the C major scale. A tritone is also commonly defined as an interval spanning six semitones. According to this definition, a diatonic scale contains two tritones for each octave. For instance, the above-mentioned C major scale contains the tritones F–B and B–F. In twelve-equal temperament, the tritone divides the octave exactly in half as 6 of 12 semitones or 600 of 1200 cents.
In modern musical notation and tuning, an enharmonic equivalent is a note, interval, or key signature that is equivalent to some other note, interval, or key signature but "spelled", or named differently. Thus, the enharmonic spelling of a written note, interval, or chord is an alternative way to write that note, interval, or chord. The term is derived from Latin enharmonicus, from Late Latin enarmonius, from Ancient Greek ἐναρμόνιος (enarmónios), from ἐν (en)+ἁρμονία (harmonía).

In music, modulation is the change from one tonality to another. This may or may not be accompanied by a change in key signature. Modulations articulate or create the structure or form of many pieces, as well as add interest. Treatment of a chord as the tonic for less than a phrase is considered tonicization.
Modulation is the essential part of the art. Without it there is little music, for a piece derives its true beauty not from the large number of fixed modes which it embraces but rather from the subtle fabric of its modulation.

Musical set theory provides concepts for categorizing musical objects and describing their relationships. Howard Hanson first elaborated many of the concepts for analyzing tonal music. Other theorists, such as Allen Forte, further developed the theory for analyzing atonal music, drawing on the twelve-tone theory of Milton Babbitt. The concepts of musical set theory are very general and can be applied to tonal and atonal styles in any equal temperament tuning system, and to some extent more generally than that.
Chromaticism is a compositional technique interspersing the primary diatonic pitches and chords with other pitches of the chromatic scale. Chromaticism is in contrast or addition to tonality or diatonicism and modality. Chromatic elements are considered, "elaborations of or substitutions for diatonic scale members".
Not only at the beginning of a composition but also in the midst of it, each scale-step [degree] manifests an irresistible urge to attain the value of the tonic for itself as that of the strongest scale-step. If the composer yields to this urge of the scale-step within the diatonic system of which this scale-step forms part, I call this process tonicalization and the phenomenon itself chromatic.
Chromaticism is almost by definition an alteration of, an interpolation in or deviation from this basic diatonic organization.
Throughout the nineteenth century, composers felt free to alter any or all chord members of a given tertian structure [chord built from thirds] according to their compositional needs and dictates. Pronounced or continuous chordal alteration [and 'extension'] resulted in chromaticism. Chromaticism, together with frequent modulations and an abundance of non-harmonicism [non-chord tones], initially effected an expansion of the tertian system; the overuse of the procedures late in the century forewarned the decline and near collapse [atonality] of the system [tonality].
Chromaticism is the name given to the use of tones outside the major or minor scales. Chromatic tones began to appear in music long before the common-practice period, and by the beginning of that period were an important part of its melodic and harmonic resources. Chromatic tones arise in music partly from inflection [alteration] of scale degrees in the major and minor modes, partly from secondary dominant harmony, from a special vocabulary of altered chords, and from certain nonharmonic tones.... Notes outside the scale do not necessarily affect the tonality....tonality is established by the progression of roots and the tonal functions of the chords, even though the details of the music may contain all the tones of the chromatic scale.
Sometimes...a melody based on a regular diatonic scale is laced with many accidentals, and although all 12 tones of the chromatic scale may appear, the tonal characteristics of the diatonic scale are maintained. ... Chromaticism [is t]he introduction of some pitches of the chromatic scale into music that is basically diatonic in orientation, or music that is based on the chromatic scale instead of the diatonic scales.
In music, transposition refers to the process or operation of moving a collection of notes up or down in pitch by a constant interval.
The shifting of a melody, a harmonic progression or an entire musical piece to another key, while maintaining the same tone structure, i.e. the same succession of whole tones and semitones and remaining melodic intervals.

In music, a closely related key is one sharing many common tones with an original key, as opposed to a distantly related key. In music harmony, there are five of them: they share all, or all except one, pitches with a key with which it is being compared, and is adjacent to it on the circle of fifths and its relative major or minor.
Modes of limited transposition are musical modes or scales that fulfill specific criteria relating to their symmetry and the repetition of their interval groups. These scales may be transposed to all twelve notes of the chromatic scale, but at least two of these transpositions must result in the same pitch classes, thus their transpositions are "limited". They were compiled by the French composer Olivier Messiaen, and published in his book La technique de mon langage musical.

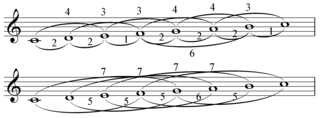
The musical operation of scalar transposition shifts every note in a melody by the same number of scale steps. The musical operation of chromatic transposition shifts every note in a melody by the same distance in pitch class space. In general, for a given scale S, the scalar transpositions of a line L can be grouped into categories, or transpositional set classes, whose members are related by chromatic transposition. In diatonic set theory cardinality equals variety when, for any melodic line L in a particular scale S, the number of these classes is equal to the number of distinct pitch classes in the line L.
In diatonic set theory structure implies multiplicity is a quality of a collection or scale. This is that for the interval series formed by the shortest distance around a diatonic circle of fifths between members of a series indicates the number of unique interval patterns formed by diatonic transpositions of that series. Structure being the intervals in relation to the circle of fifths, multiplicity being the number of times each different (adjacent) interval pattern occurs. The property was first described by John Clough and Gerald Myerson in "Variety and Multiplicity in Diatonic Systems" (1985).
In diatonic set theory, a generated collection is a collection or scale formed by repeatedly adding a constant interval in integer notation, the generator, also known as an interval cycle, around the chromatic circle until a complete collection or scale is formed. All scales with the deep scale property can be generated by any interval coprime with twelve.

In diatonic set theory a generic interval is the number of scale steps between notes of a collection or scale. The largest generic interval is one less than the number of scale members.

In musical set theory, an interval vector is an array of natural numbers which summarize the intervals present in a set of pitch classes. Other names include: ic vector, PIC vector and APIC vector
In diatonic set theory, Rothenberg propriety is an important concept, lack of contradiction and ambiguity, in the general theory of musical scales which was introduced by David Rothenberg in a seminal series of papers in 1978. The concept was independently discovered in a more restricted context by Gerald Balzano, who termed it coherence.

Music theory has no axiomatic foundation in modern mathematics, although some interesting work has recently been done in this direction, yet the basis of musical sound can be described mathematically and exhibits "a remarkable array of number properties". Elements of music such as its form, rhythm and metre, the pitches of its notes and the tempo of its pulse can be related to the measurement of time and frequency, offering ready analogies in geometry.

Diatonic and chromatic are terms in music theory that are most often used to characterize scales, and are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900.