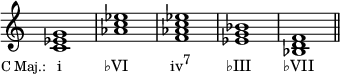In music theory, the term mode or modus is used in a number of distinct senses, depending on context.

The major scale is one of the most commonly used musical scales, especially in Western music. It is one of the diatonic scales. Like many musical scales, it is made up of seven notes: the eighth duplicates the first at double its frequency so that it is called a higher octave of the same note.
In western classical music theory, the minor scale refers to three scale patterns – the natural minor scale, the harmonic minor scale, and the melodic minor scale.
In music theory, a leading-tone is a note or pitch which resolves or "leads" to a note one semitone higher or lower, being a lower and upper leading-tone, respectively. Typically, the leading tone refers to the seventh scale degree of a major scale, a major seventh above the tonic. In the movable do solfège system, the leading-tone is sung as ti.
An altered chord is a chord that replaces one or more notes from the diatonic scale with a neighboring pitch from the chromatic scale. By the broadest definition, any chord with a non-diatonic chord tone is an altered chord. The simplest example of altered chords is the use of borrowed chords, chords borrowed from the parallel key, and the most common is the use of secondary dominants. As Alfred Blatter explains, "An altered chord occurs when one of the standard, functional chords is given another quality by the modification of one or more components of the chord."
In a musical composition, a chord progression or harmonic progression is a succession of chords. Chord progressions are the foundation of harmony in Western musical tradition from the common practice era of Classical music to the 21st century. Chord progressions are the foundation of popular music styles, traditional music, as well as genres such as blues and jazz. In these genres, chord progressions are the defining feature on which melody and rhythm are built.

In music, a chord is a group of two or more notes played simultaneously, typically consisting of a root note, a third, and a fifth. Chords are the building blocks of harmony and form the harmonic foundation of a piece of music. They can be major, minor, diminished, augmented, or extended, depending on the intervals between the notes and their arrangement. Chords provide the harmonic support and coloration that accompany melodies and contribute to the overall sound and mood of a musical composition. For many practical and theoretical purposes, arpeggios and other types of broken chords may also be considered as chords in the right musical context.

In music, modulation is the change from one tonality to another. This may or may not be accompanied by a change in key signature. Modulations articulate or create the structure or form of many pieces, as well as add interest. Treatment of a chord as the tonic for less than a phrase is considered tonicization.
Modulation is the essential part of the art. Without it there is little music, for a piece derives its true beauty not from the large number of fixed modes which it embraces but rather from the subtle fabric of its modulation.
A secondary chord is an analytical label for a specific harmonic device that is prevalent in the tonal idiom of Western music beginning in the common practice period: the use of diatonic functions for tonicization.
In music, the submediant is the sixth degree of a diatonic scale. The submediant is named thus because it is halfway between the tonic and the subdominant or because its position below the tonic is symmetrical to that of the mediant above.

In music, the supertonic is the second degree of a diatonic scale, one whole step above the tonic. In the movable do solfège system, the supertonic note is sung as re.
In music, the subtonic is the degree of a musical scale which is a whole step below the tonic note. In a major key, it is a lowered, or flattened, seventh scale degree. It appears as the seventh scale degree in the natural minor and descending melodic minor scales but not in the major scale. In major keys, the subtonic sometimes appears in borrowed chords. In the movable do solfège system, the subtonic note is sung as te.
Chromaticism is a compositional technique interspersing the primary diatonic pitches and chords with other pitches of the chromatic scale. In simple terms, within each octave, diatonic music uses only seven different notes, rather than the twelve available on a standard piano keyboard. Music is chromatic when it uses more than just these seven notes.
The Aeolian mode is a musical mode or, in modern usage, a diatonic scale also called the natural minor scale. On the piano, using only the white keys, it is the scale that starts with A and continues to the next A only striking white keys. Its ascending interval form consists of a key note, whole step, half step, whole step, whole step, half step, whole step, whole step. That means that, in A aeolian, you would play A, move up a whole step to B, move up a half step to C, then up a whole step to D, a whole step to E, a half step to F, a whole step to G, and a final whole step to a high A.
In music, a minor seventh chord is a seventh chord composed of a root note, a minor third, a perfect fifth, and a minor seventh. In other words, one could think of it as a minor triad with a minor seventh attached to it.

In music theory, the harmonic major scale is a musical scale found in some music from the common practice era and now used occasionally, most often in jazz. It corresponds to the Raga Sarasangi in Indian Carnatic music, or Raag Nat Bhairav in Hindustani music.

The Andalusian cadence is a term adopted from flamenco music for a chord progression comprising four chords descending stepwise – a iv–III–II–I progression with respect to the Phrygian mode or i–VII–VI–V progression with respect to the Aeolian mode (minor). It is otherwise known as the minor descending tetrachord. Traceable back to the Renaissance, its effective sonorities made it one of the most popular progressions in classical music.

Diatonic and chromatic are terms in music theory that are used to characterize scales. The terms are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900.

In music, chromatic mediants are "altered mediant and submediant chords." A chromatic mediant relationship defined conservatively is a relationship between two sections and/or chords whose roots are related by a major third or minor third, and contain one common tone. For example, in the key of C major the diatonic mediant and submediant are E minor and A minor respectively. Their parallel majors are E major and A major. The mediants of the parallel minor of C major are E♭ major and A♭ major. Thus, by this conservative definition, C major has four chromatic mediants: E major, A major, E♭ major, and A♭ major.
In music theory, Roman numeral analysis is a type of harmonic analysis in which chords are represented by Roman numerals, which encode the chord's degree and harmonic function within a given musical key.