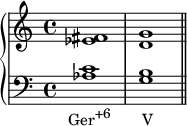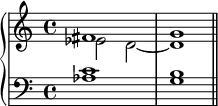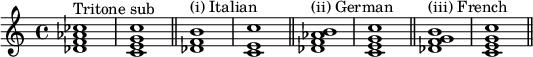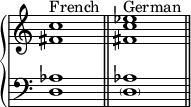The major scale is one of the most commonly used musical scales, especially in Western music. It is one of the diatonic scales. Like many musical scales, it is made up of seven notes: the eighth duplicates the first at double its frequency so that it is called a higher octave of the same note.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.
In music theory, the tritone is defined as a musical interval spanning three adjacent whole tones. For instance, the interval from F up to the B above it is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B.
An altered chord is a chord that replaces one or more notes from the diatonic scale with a neighboring pitch from the chromatic scale. By the broadest definition, any chord with a non-diatonic chord tone is an altered chord. The simplest example of altered chords is the use of borrowed chords, chords borrowed from the parallel key, and the most common is the use of secondary dominants. As Alfred Blatter explains, "An altered chord occurs when one of the standard, functional chords is given another quality by the modification of one or more components of the chord."
A seventh chord is a chord consisting of a triad plus a note forming an interval of a seventh above the chord's root. When not otherwise specified, a "seventh chord" usually means a dominant seventh chord: a major triad together with a minor seventh. However, a variety of sevenths may be added to a variety of triads, resulting in many different types of seventh chords.

In music, a chord is a group of three or more notes played simultaneously, typically consisting of a root note, a third, and a fifth. Chords are the building blocks of harmony and form the harmonic foundation of a piece of music. They can be major, minor, diminished, augmented, or extended, depending on the intervals between the notes and their arrangement. Chords provide the harmonic support and coloration that accompany melodies and contribute to the overall sound and mood of a musical composition. For many practical and theoretical purposes, arpeggios and other types of broken chords may also be considered as chords in the right musical context.

In music, modulation is the change from one tonality to another. This may or may not be accompanied by a change in key signature. Modulations articulate or create the structure or form of many pieces, as well as add interest. Treatment of a chord as the tonic for less than a phrase is considered tonicization.
Modulation is the essential part of the art. Without it there is little music, for a piece derives its true beauty not from the large number of fixed modes which it embraces but rather from the subtle fabric of its modulation.

A semitone, also called a minor second, half step, or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale, visually seen on a keyboard as the distance between two keys that are adjacent to each other. For example, C is adjacent to C♯; the interval between them is a semitone.

In Western classical music, an augmented fifth is an interval produced by widening a perfect fifth by a chromatic semitone. For instance, the interval from C to G is a perfect fifth, seven semitones wide, and both the intervals from C♭ to G, and from C to G♯ are augmented fifths, spanning eight semitones. Being augmented, it is considered a dissonant interval.
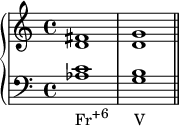
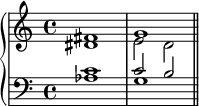
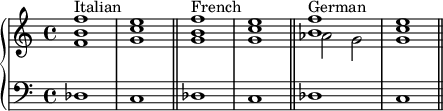
In Classical music theory, a Neapolitan chord is a major chord built on the lowered (flattened) second (supertonic) scale degree. In Schenkerian analysis, it is known as a Phrygian II, since in minor scales the chord is built on the notes of the corresponding Phrygian mode.
The diminished seventh chord is a four-note chord composed of a root note, together with a minor third, a diminished fifth, and a diminished seventh above the root:. For example, the diminished seventh chord built on B, commonly written as Bo7, has pitches B-D-F-A♭:

In music, an augmented sixth is an interval produced by widening a major sixth by a chromatic semitone. For instance, the interval from C to A is a major sixth, nine semitones wide, and both the intervals from C♭ to A, and from C to A♯ are augmented sixths, spanning ten semitones. Being augmented, it is considered a dissonant interval.

In classical music from Western culture, an augmented second is an interval that, in 12-tone equal temperament, is sonically equivalent to a minor third, spanning three semitones, and is created by widening a major second by a chromatic semitone. For instance, the interval from C to D is a major second, two semitones wide, and the interval from C to D♯ is an augmented second, spanning three semitones.

In music theory, the harmonic major scale is a musical scale found in some music from the common practice era and now used occasionally, most often in jazz. It corresponds to the Raga Sarasangi in Indian Carnatic music, or Raag Nat Bhairav in Hindustani music.
The harmonic minor scale is a musical scale derived from the natural minor scale, with the minor seventh degree raised by one semitone to a major seventh, creating an augmented second between the sixth and seventh degrees.
In music theory, the half-diminished seventh chord is a seventh chord composed of a root note, together with a minor third, a diminished fifth, and a minor seventh. For example, the half-diminished seventh chord built on B, commonly written as Bm7(♭5), or Bø7, has pitches B-D-F-A:

Diatonic and chromatic are terms in music theory that are used to characterize scales. The terms are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900.

In music, an irregular resolution is resolution by a dominant seventh chord or diminished seventh chord to a chord other than the tonic. Regarding the dominant seventh, there are many irregular resolutions including to a chord with which it has tones in common or if the parts move only a whole or half step. Consecutive fifths and octaves, augmented intervals, and false relations should still be avoided. Voice leading may cause the seventh to ascend, to be prolonged into the next chord, or to be unresolved.
In music, harmonization is the chordal accompaniment to a line or melody: "Using chords and melodies together, making harmony by stacking scale tones as triads".
Musicians use various kinds of chord names and symbols in different contexts to represent musical chords. In most genres of popular music, including jazz, pop, and rock, a chord name and its corresponding symbol typically indicate one or more of the following: