Genetic drift, also known as random genetic drift, allelic drift or the Wright effect, is the change in the frequency of an existing gene variant (allele) in a population due to random chance.
Population genetics is a subfield of genetics that deals with genetic differences within and among populations, and is a part of evolutionary biology. Studies in this branch of biology examine such phenomena as adaptation, speciation, and population structure.
Genetic linkage is the tendency of DNA sequences that are close together on a chromosome to be inherited together during the meiosis phase of sexual reproduction. Two genetic markers that are physically near to each other are unlikely to be separated onto different chromatids during chromosomal crossover, and are therefore said to be more linked than markers that are far apart. In other words, the nearer two genes are on a chromosome, the lower the chance of recombination between them, and the more likely they are to be inherited together. Markers on different chromosomes are perfectly unlinked, although the penetrance of potentially deleterious alleles may be influenced by the presence of other alleles, and these other alleles may be located on other chromosomes than that on which a particular potentially deleterious allele is located.
A genetic screen or mutagenesis screen is an experimental technique used to identify and select individuals who possess a phenotype of interest in a mutagenized population. Hence a genetic screen is a type of phenotypic screen. Genetic screens can provide important information on gene function as well as the molecular events that underlie a biological process or pathway. While genome projects have identified an extensive inventory of genes in many different organisms, genetic screens can provide valuable insight as to how those genes function.
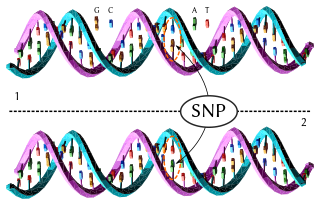
In genetics and bioinformatics, a single-nucleotide polymorphism is a germline substitution of a single nucleotide at a specific position in the genome. Although certain definitions require the substitution to be present in a sufficiently large fraction of the population, many publications do not apply such a frequency threshold.

A haplotype is a group of alleles in an organism that are inherited together from a single parent.
In biology and genetic genealogy, the most recent common ancestor (MRCA), also known as the last common ancestor (LCA), of a set of organisms is the most recent individual from which all the organisms of the set are descended. The term is also used in reference to the ancestry of groups of genes (haplotypes) rather than organisms.
In population genetics, Ewens's sampling formula describes the probabilities associated with counts of how many different alleles are observed a given number of times in the sample.
The effective population size (Ne) is the size of an idealised population that would experience the same rate of genetic drift as the real population. The effective population size is normally smaller than the census population size N, partly because chance events prevent some individuals from breeding, and partly due to background selection and genetic hitchhiking. Idealised populations are based on unrealistic but convenient assumptions including random mating, rarity of natural selection such that each gene evolves independently, and constant population size.
Genetics, a discipline of biology, is the science of heredity and variation in living organisms.
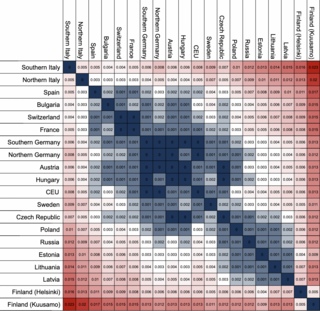
The fixation index (FST) is a measure of population differentiation due to genetic structure. It is frequently estimated from genetic polymorphism data, such as single-nucleotide polymorphisms (SNP) or microsatellites. Developed as a special case of Wright's F-statistics, it is one of the most commonly used statistics in population genetics. Its values range from 0 to 1, with 0 being no differentiation and 1 being complete differentiation.
Background selection describes the loss of genetic diversity at a locus due to negative selection against deleterious alleles with which it is in linkage disequilibrium. The name emphasizes the fact that the genetic background, or genomic environment, of a mutation has a significant impact on whether it will be preserved versus lost from a population. Background selection contradicts the assumption of the neutral theory of molecular evolution that the fixation or loss of a neutral allele can be described by one-locus models of genetic drift, independently from other loci. As well as reducing neutral nucleotide diversity, background selection reduces the fixation probability of beneficial mutations, and increases the fixation probability of deleterious mutations.
In population genetics, fixation is the change in a gene pool from a situation where there exists at least two variants of a particular gene (allele) in a given population to a situation where only one of the alleles remains. That is, the allele becomes fixed. In the absence of mutation or heterozygote advantage, any allele must eventually either be lost completely from the population, or fixed, i.e. permanently established at 100% frequency in the population. Whether a gene will ultimately be lost or fixed is dependent on selection coefficients and chance fluctuations in allelic proportions. Fixation can refer to a gene in general or particular nucleotide position in the DNA chain (locus).
A genetic lineage includes all descendants of a given genetic sequence, typically following a new mutation. It is not the same as an allele because it excludes cases where different mutations give rise to the same allele, and includes descendants that differ from the ancestor by one or more mutations. The genetic sequence can be of different sizes, e.g. a single gene or a haplotype containing multiple adjacent genes along a chromosome. Given recombination, each gene can have a separate genetic lineages, even as the population shares a single organismal lineage. In asexual microbes or somatic cells, cell lineages exactly match genetic lineages, and can be traced.
Viral phylodynamics is the study of how epidemiological, immunological, and evolutionary processes act and potentially interact to shape viral phylogenies. Since the term was coined in 2004, research on viral phylodynamics has focused on transmission dynamics in an effort to shed light on how these dynamics impact viral genetic variation. Transmission dynamics can be considered at the level of cells within an infected host, individual hosts within a population, or entire populations of hosts.
In population genetics, the allele frequency spectrum, sometimes called the site frequency spectrum, is the distribution of the allele frequencies of a given set of loci in a population or sample. Because an allele frequency spectrum is often a summary of or compared to sequenced samples of the whole population, it is a histogram with size depending on the number of sequenced individual chromosomes. Each entry in the frequency spectrum records the total number of loci with the corresponding derived allele frequency. Loci contributing to the frequency spectrum are assumed to be independently changing in frequency. Furthermore, loci are assumed to be biallelic, although extensions for multiallelic frequency spectra exist.
The Infinite sites model (ISM) is a mathematical model of molecular evolution first proposed by Motoo Kimura in 1969. Like other mutation models, the ISM provides a basis for understanding how mutation develops new alleles in DNA sequences. Using allele frequencies, it allows for the calculation of heterozygosity, or genetic diversity, in a finite population and for the estimation of genetic distances between populations of interest.
Multispecies Coalescent Process is a stochastic process model that describes the genealogical relationships for a sample of DNA sequences taken from several species. It represents the application of coalescent theory to the case of multiple species. The multispecies coalescent results in cases where the relationships among species for an individual gene can differ from the broader history of the species. It has important implications for the theory and practice of phylogenetics and for understanding genome evolution.
Allele age is the amount of time elapsed since an allele first appeared due to mutation. Estimating the time at which a certain allele appeared allows researchers to infer patterns of human migration, disease, and natural selection. Allele age can be estimated based on (1) the frequency of the allele in a population and (2) the genetic variation that occurs within different copies of the allele, also known as intra-allelic variation. While either of these methods can be used to estimate allele age, the use of both increases the accuracy of the estimation and can sometimes offer additional information regarding the presence of selection.
This glossary of genetics and evolutionary biology is a list of definitions of terms and concepts used in the study of genetics and evolutionary biology, as well as sub-disciplines and related fields, with an emphasis on classical genetics, quantitative genetics, population biology, phylogenetics, speciation, and systematics. It has been designed as a companion to Glossary of cellular and molecular biology, which contains many overlapping and related terms; other related glossaries include Glossary of biology and Glossary of ecology.







