
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz.

In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
- The laws of physics are invariant in all inertial frames of reference.
- The speed of light in vacuum is the same for all observers, regardless of the motion of the light source or observer.

In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine details of the hydrogen spectrum in a completely rigorous way.
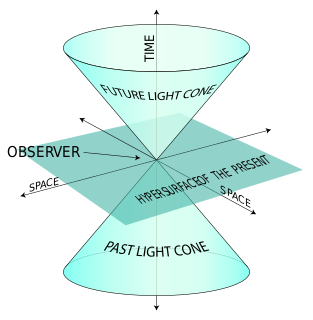
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime. The contravariant four-momentum of a particle with relativistic energy E and three-momentum p = = γmv, where v is the particle's three-velocity and γ the Lorentz factor, is

In special relativity, a four-vector is an object with four components, which transform in a specific way under Lorentz transformation. Specifically, a four-vector is an element of a four-dimensional vector space considered as a representation space of the standard representation of the Lorentz group, the representation. It differs from a Euclidean vector in how its magnitude is determined. The transformations that preserve this magnitude are the Lorentz transformations, which include spatial rotations and boosts.
In relativistic physics, Lorentz symmetry, named after Hendrik Lorentz, is an equivalence of observation or observational symmetry due to special relativity implying that the laws of physics stay the same for all observers that are moving with respect to one another within an inertial frame. It has also been described as "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space".
In mathematical physics, the conformal symmetry of spacetime is expressed by an extension of the Poincaré group. The extension includes special conformal transformations and dilations. In three spatial plus one time dimensions, conformal symmetry has 15 degrees of freedom: ten for the Poincaré group, four for special conformal transformations, and one for a dilation.
In special and general relativity, the four-current is the four-dimensional analogue of the electric current density. Also known as vector current, it is used in the geometric context of four-dimensional spacetime, rather than three-dimensional space and time separately. Mathematically it is a four-vector, and is Lorentz covariant.

The mathematics of general relativity refers to various mathematical structures and techniques that are used in studying and formulating Albert Einstein's theory of general relativity. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.

In electromagnetism, the electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field in spacetime. The field tensor was first used after the four-dimensional tensor formulation of special relativity was introduced by Hermann Minkowski. The tensor allows related physical laws to be written very concisely.
In general relativity, the hole argument is an apparent paradox that much troubled Albert Einstein while developing his famous field equations.

In physics, a symmetry of a physical system is a physical or mathematical feature of the system that is preserved or remains unchanged under some transformation.
In physics, the Majorana equation is a relativistic wave equation. It is named after the Italian physicist Ettore Majorana, who proposed it in 1937 as a means of describing fermions that are their own antiparticle. Particles corresponding to this equation are termed Majorana particles, although that term now has a more expansive meaning, referring to any fermionic particle that is its own anti-particle.
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the affine connection. It can also be regarded as the gauge field generated by local Lorentz transformations. In some canonical formulations of general relativity, a spin connection is defined on spatial slices and can also be regarded as the gauge field generated by local rotations.

In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system. These equations can be viewed as a generalization of the vacuum Maxwell's equations which are normally formulated in the local coordinates of flat spacetime. But because general relativity dictates that the presence of electromagnetic fields induce curvature in spacetime, Maxwell's equations in flat spacetime should be viewed as a convenient approximation.
In physics, the principle of covariance emphasizes the formulation of physical laws using only those physical quantities the measurements of which the observers in different frames of reference could unambiguously correlate.
In mathematical physics, the Dirac algebra is the Clifford algebra Cℓ4(C), which may be thought of as Cℓ1,3(C). This was introduced by the mathematical physicist P. A. M. Dirac in 1928 in developing the Dirac equation for spin-½ particles with a matrix representation with the Dirac gamma matrices, which represent the generators of the algebra.

The theory of special relativity plays an important role in the modern theory of classical electromagnetism. It gives formulas for how electromagnetic objects, in particular the electric and magnetic fields, are altered under a Lorentz transformation from one inertial frame of reference to another. It sheds light on the relationship between electricity and magnetism, showing that frame of reference determines if an observation follows electrostatic or magnetic laws. It motivates a compact and convenient notation for the laws of electromagnetism, namely the "manifestly covariant" tensor form.

In physics, a gauge theory is a type of field theory in which the Lagrangian does not change under local transformations according to certain smooth families of operations.

In physics, particularly in quantum field theory, the Weyl equation is a relativistic wave equation for describing massless spin-1/2 particles called Weyl fermions. The equation is named after Hermann Weyl. The Weyl fermions are one of the three possible types of elementary fermions, the other two being the Dirac and the Majorana fermions.










