
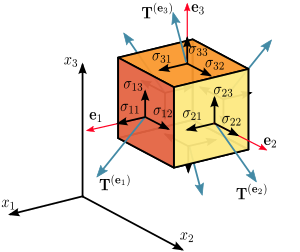
The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields. This density and flux of energy and momentum are the sources of the gravitational field in the Einstein field equations of general relativity, just as mass density is the source of such a field in Newtonian gravity.
In Einstein's theory of general relativity, the Schwarzschild metric is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916.
The Penrose–Hawking singularity theorems are a set of results in general relativity that attempt to answer the question of when gravitation produces singularities. The Penrose singularity theorem is a theorem in semi-Riemannian geometry and its general relativistic interpretation predicts a gravitational singularity in black hole formation. The Hawking singularity theorem is based on the Penrose theorem and it is interpreted as a gravitational singularity in the Big Bang situation. Penrose shared half of the Nobel Prize in Physics in 2020 "for the discovery that black hole formation is a robust prediction of the general theory of relativity".
In the general theory of relativity, the Einstein field equations relate the geometry of spacetime to the distribution of matter within it.
Teleparallelism, was an attempt by Albert Einstein to base a unified theory of electromagnetism and gravity on the mathematical structure of distant parallelism, also referred to as absolute or teleparallelism. In this theory, a spacetime is characterized by a curvature-free linear connection in conjunction with a metric tensor field, both defined in terms of a dynamical tetrad field.
In differential geometry, the Einstein tensor is used to express the curvature of a pseudo-Riemannian manifold. In general relativity, it occurs in the Einstein field equations for gravitation that describe spacetime curvature in a manner that is consistent with conservation of energy and momentum.
In general relativity, a vacuum solution is a Lorentzian manifold whose Einstein tensor vanishes identically. According to the Einstein field equation, this means that the stress–energy tensor also vanishes identically, so that no matter or non-gravitational fields are present. These are distinct from the electrovacuum solutions, which take into account the electromagnetic field in addition to the gravitational field. Vacuum solutions are also distinct from the lambdavacuum solutions, where the only term in the stress–energy tensor is the cosmological constant term.
In general relativity, the pp-wave spacetimes, or pp-waves for short, are an important family of exact solutions of Einstein's field equation. The term pp stands for plane-fronted waves with parallel propagation, and was introduced in 1962 by Jürgen Ehlers and Wolfgang Kundt.
In physics and mathematics, a pseudotensor is usually a quantity that transforms like a tensor under an orientation-preserving coordinate transformation but additionally changes sign under an orientation-reversing coordinate transformation, which is a transformation that can be expressed as a proper rotation followed by reflection. This is a generalization of a pseudovector. To evaluate a tensor or pseudotensor sign, it has to be contracted with some vectors, as many as its rank is, belonging to the space where the rotation is made while keeping the tensor coordinates unaffected. Under improper rotation a pseudotensor and a proper tensor of the same rank will have different sign which depends on the rank being even or odd. Sometimes inversion of the axes is used as an example of an improper rotation to see the behaviour of a pseudotensor, but it works only if vector space dimensions is odd otherwise inversion is a proper rotation without an additional reflection.
When studying and formulating Albert Einstein's theory of general relativity, various mathematical structures and techniques are utilized. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.
Spacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems. Spacetime symmetries are used in the study of exact solutions of Einstein's field equations of general relativity. Spacetime symmetries are distinguished from internal symmetries.
In general relativity, the metric tensor is the fundamental object of study. The metric captures all the geometric and causal structure of spacetime, being used to define notions such as time, distance, volume, curvature, angle, and separation of the future and the past.
In general relativity, if two objects are set in motion along two initially parallel trajectories, the presence of a tidal gravitational force will cause the trajectories to bend towards or away from each other, producing a relative acceleration between the objects.
In theoretical physics, Nordström's theory of gravitation was a predecessor of general relativity. Strictly speaking, there were actually two distinct theories proposed by the Finnish theoretical physicist Gunnar Nordström, in 1912 and 1913 respectively. The first was quickly dismissed, but the second became the first known example of a metric theory of gravitation, in which the effects of gravitation are treated entirely in terms of the geometry of a curved spacetime.
A theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity by examining the dynamics of particles in circular orbits about the Earth. A key advantage in examining circular orbits is that it is possible to know the solution of the Einstein Field Equation a priori. This provides a means to inform and verify the formalism.
This article will use the Einstein summation convention.
In general relativity, the laws of physics can be expressed in a generally covariant form. In other words, the description of the world as given by the laws of physics does not depend on our choice of coordinate systems. However, it is often useful to fix upon a particular coordinate system, in order to solve actual problems or make actual predictions. A coordinate condition selects such coordinate system(s).
Gauge theory gravity (GTG) is a theory of gravitation cast in the mathematical language of geometric algebra. To those familiar with general relativity, it is highly reminiscent of the tetrad formalism although there are significant conceptual differences. Most notably, the background in GTG is flat, Minkowski spacetime. The equivalence principle is not assumed, but instead follows from the fact that the gauge covariant derivative is minimally coupled. As in general relativity, equations structurally identical to the Einstein field equations are derivable from a variational principle. A spin tensor can also be supported in a manner similar to Einstein–Cartan–Sciama–Kibble theory. GTG was first proposed by Lasenby, Doran, and Gull in 1998 as a fulfillment of partial results presented in 1993. The theory has not been widely adopted by the rest of the physics community, who have mostly opted for differential geometry approaches like that of the related gauge gravitation theory.




![Example: Parallel displacement along a circle of a three-dimensional ball embedded in two dimensions. The circle of radius r is embedded in a two-dimensional space characterized by the coordinates z and z. The circle itself is characterized by coordinates y and y in the two-dimensional space. The circle itself is one-dimensional and can be characterized by its arc length x. The coordinate y is related to the coordinate x through the relation y = r cos
.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}
x/r and y = r sin
x/r. This gives
[?]y/[?]x = -sin
x/r and
[?]y/[?]x = cos
x/r In this case the metric is a scalar and is given by g = cos
x/r + sin
x/r = 1. The interval is then ds = g dx = dx. The interval is just equal to the arc length as expected. Parallel displacement.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/7/7c/Parallel_displacement.svg/450px-Parallel_displacement.svg.png)




