In physics, physical optics, or wave optics, is the branch of optics that studies interference, diffraction, polarization, and other phenomena for which the ray approximation of geometric optics is not valid. This usage tends not to include effects such as quantum noise in optical communication, which is studied in the sub-branch of coherence theory.
Physical optics is also the name of an approximation commonly used in optics, electrical engineering and applied physics. In this context, it is an intermediate method between geometric optics, which ignores wave effects, and full wave electromagnetism, which is a precise theory. The word "physical" means that it is more physical than geometric or ray optics and not that it is an exact physical theory. [1] : 11–13
This approximation consists of using ray optics to estimate the field on a surface and then integrating that field over the surface to calculate the transmitted or scattered field. This resembles the Born approximation, in that the details of the problem are treated as a perturbation.
In optics, it is a standard way of estimating diffraction effects. In radio, this approximation is used to estimate some effects that resemble optical effects. It models several interference, diffraction and polarization effects but not the dependence of diffraction on polarization. Since this is a high-frequency approximation, it is often more accurate in optics than for radio.
In optics, it typically consists of integrating ray-estimated field over a lens, mirror or aperture to calculate the transmitted or scattered field.
In radar scattering it usually means taking the current that would be found on a tangent plane of similar material as the current at each point on the front, i. e. the geometrically illuminated part, of a scatterer. Current on the shadowed parts is taken as zero. The approximate scattered field is then obtained by an integral over these approximate currents. This is useful for bodies with large smooth convex shapes and for lossy (low-reflection) surfaces.
The ray-optics field or current is generally not accurate near edges or shadow boundaries, unless supplemented by diffraction and creeping wave calculations.
The standard theory of physical optics has some defects in the evaluation of scattered fields, leading to decreased accuracy away from the specular direction. [2] [3] An improved theory introduced in 2004 gives exact solutions to problems involving wave diffraction by conducting scatterers. [2]
The Huygens–Fresnel principle states that every point on a wavefront is itself the source of spherical wavelets, and the secondary wavelets emanating from different points mutually interfere. The sum of these spherical wavelets forms a new wavefront. As such, the Huygens-Fresnel principle is a method of analysis applied to problems of luminous wave propagation both in the far-field limit and in near-field diffraction as well as reflection.
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet, and infrared light. Light is a type of electromagnetic radiation, and other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties.
Polarization is a property of transverse waves which specifies the geometrical orientation of the oscillations. In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave. A simple example of a polarized transverse wave is vibrations traveling along a taut string (see image); for example, in a musical instrument like a guitar string. Depending on how the string is plucked, the vibrations can be in a vertical direction, horizontal direction, or at any angle perpendicular to the string. In contrast, in longitudinal waves, such as sound waves in a liquid or gas, the displacement of the particles in the oscillation is always in the direction of propagation, so these waves do not exhibit polarization. Transverse waves that exhibit polarization include electromagnetic waves such as light and radio waves, gravitational waves, and transverse sound waves in solids.
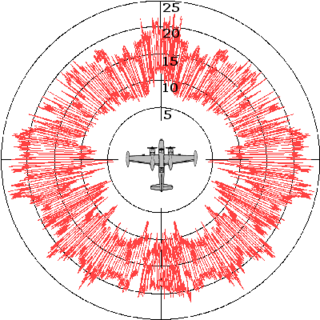
Radar cross-section (RCS), denoted σ, also called radar signature, is a measure of how detectable an object is by radar. A larger RCS indicates that an object is more easily detected.
A metamaterial is any material engineered to have a property that is rarely observed in naturally occurring materials. They are made from assemblies of multiple elements fashioned from composite materials such as metals and plastics. These materials are usually arranged in repeating patterns, at scales that are smaller than the wavelengths of the phenomena they influence. Metamaterials derive their properties not from the properties of the base materials, but from their newly designed structures. Their precise shape, geometry, size, orientation and arrangement gives them their smart properties capable of manipulating electromagnetic waves: by blocking, absorbing, enhancing, or bending waves, to achieve benefits that go beyond what is possible with conventional materials.
Finite-difference time-domain (FDTD) or Yee's method is a numerical analysis technique used for modeling computational electrodynamics. Since it is a time-domain method, FDTD solutions can cover a wide frequency range with a single simulation run, and treat nonlinear material properties in a natural way.
A high-frequency approximation for scattering or other wave propagation problems, in physics or engineering, is an approximation whose accuracy increases with the size of features on the scatterer or medium relative to the wavelength of the scattered particles.
In optics, a ray is an idealized geometrical model of light or other electromagnetic radiation, obtained by choosing a curve that is perpendicular to the wavefronts of the actual light, and that points in the direction of energy flow. Rays are used to model the propagation of light through an optical system, by dividing the real light field up into discrete rays that can be computationally propagated through the system by the techniques of ray tracing. This allows even very complex optical systems to be analyzed mathematically or simulated by computer. Ray tracing uses approximate solutions to Maxwell's equations that are valid as long as the light waves propagate through and around objects whose dimensions are much greater than the light's wavelength. Ray optics or geometrical optics does not describe phenomena such as diffraction, which require wave optics theory. Some wave phenomena such as interference can be modeled in limited circumstances by adding phase to the ray model.
Computational electromagnetics (CEM), computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment using computers.
A Bessel beam is a wave whose amplitude is described by a Bessel function of the first kind. Electromagnetic, acoustic, gravitational, and matter waves can all be in the form of Bessel beams. A true Bessel beam is non-diffractive. This means that as it propagates, it does not diffract and spread out; this is in contrast to the usual behavior of light, which spreads out after being focused down to a small spot. Bessel beams are also self-healing, meaning that the beam can be partially obstructed at one point, but will re-form at a point further down the beam axis.
In physics, ray tracing is a method for calculating the path of waves or particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, change direction, or reflect off surfaces, complicating analysis. Strictly speaking Ray tracing is when analytic solutions to the ray's trajectories are solved; however Ray tracing is often confused with ray-marching which numerically solves problems by repeatedly advancing idealized narrow beams called rays through the medium by discrete amounts. Simple problems can be analyzed by propagating a few rays using simple mathematics. More detailed analysis can be performed by using a computer to propagate many rays.
The history of metamaterials begins with artificial dielectrics in microwave engineering as it developed just after World War II. Yet, there are seminal explorations of artificial materials for manipulating electromagnetic waves at the end of the 19th century. Hence, the history of metamaterials is essentially a history of developing certain types of manufactured materials, which interact at radio frequency, microwave, and later optical frequencies.
An electromagnetic metasurface refers to a kind of artificial sheet material with sub-wavelength thickness. Metasurfaces can be either structured or unstructured with subwavelength-scaled patterns in the horizontal dimensions.
The shooting and bouncing rays (SBR) method in computational electromagnetics was first developed for computation of radar cross section (RCS). Since then, the method has been generalized to be used also for installed antenna performance. The SBR method is an approximate method applied to high frequencies. The method can be implemented for GPU computing, which makes the computation very efficient.
Weng Cho Chew is a Malaysian-American electrical engineer and applied physicist known for contributions to wave physics, especially computational electromagnetics. He is a Distinguished Professor of Electrical and Computer Engineering at Purdue University.
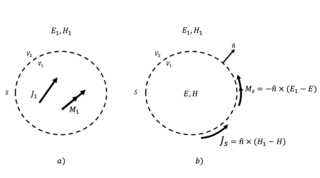
In electromagnetism, surface equivalence principle or surface equivalence theorem relates an arbitrary current distribution within an imaginary closed surface with an equivalent source on the surface. It is also known as field equivalence principle, Huygens' equivalence principle or simply as the equivalence principle. Being a more rigorous reformulation of the Huygens–Fresnel principle, it is often used to simplify the analysis of radiating structures such as antennas.
The method of moments (MoM), also known as the moment method and method of weighted residuals, is a numerical method in computational electromagnetics. It is used in computer programs that simulate the interaction of electromagnetic fields such as radio waves with matter, for example antenna simulation programs like NEC that calculate the radiation pattern of an antenna. Generally being a frequency-domain method, it involves the projection of an integral equation into a system of linear equations by the application of appropriate boundary conditions. This is done by using discrete meshes as in finite difference and finite element methods, often for the surface. The solutions are represented with the linear combination of pre-defined basis functions; generally, the coefficients of these basis functions are the sought unknowns. Green's functions and Galerkin method play a central role in the method of moments.
Georges Armand Deschamps was a French American engineer and Professor Emeritus at the Department of Electrical Engineering at University of Illinois at Urbana-Champaign. He is best known for his contributions to electromagnetic theory, microwave engineering and antenna theory. He is also regarded as an early pioneer of microstrip and patch antennas, which he proposed in 1953.
Akira Ishimaru is a Japanese-American electrical engineer and professor emeritus at Department of Electrical and Computer Engineering at University of Washington. He is best known for his contributions to the theory of wave scattering in random media.
Media related to Physical optics at Wikimedia Commons| Authority control databases: National |
|---|
