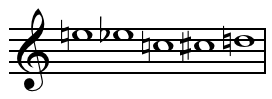In music, a tone row or note row, also series or set, is a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets are sometimes found.

The chromatic scale is a set of twelve pitches used in tonal music, with notes separated by the interval of a semitone. Almost all western musical instruments, such as the piano, are made to produce the chromatic scale, while other instruments capable of continuously variable pitch, such as the trombone and violin, can also produce microtones, or notes between those available on a piano.

The twelve-tone technique—also known as dodecaphony, twelve-tone serialism, and twelve-note composition—is a method of musical composition first devised by Austrian composer Josef Matthias Hauer, who published his "law of the twelve tones" in 1919. In 1923, Arnold Schoenberg (1874–1951) developed his own, better-known version of 12-tone technique, which became associated with the "Second Viennese School" composers, who were the primary users of the technique in the first decades of its existence. The technique is a means of ensuring that all 12 notes of the chromatic scale are sounded as often as one another in a piece of music while preventing the emphasis of any one note through the use of tone rows, orderings of the 12 pitch classes. All 12 notes are thus given more or less equal importance, and the music avoids being in a key. Over time, the technique increased greatly in popularity and eventually became widely influential on 20th-century composers. Many important composers who had originally not subscribed to or actively opposed the technique, such as Aaron Copland and Igor Stravinsky, eventually adopted it in their music.
An octatonic scale is any eight-note musical scale. However, the term most often refers to the symmetric scale composed of alternating whole and half steps, as shown at right. In classical theory, this scale is commonly called the octatonic scale, although there are a total of 42 enharmonically non-equivalent, transpositionally non-equivalent eight-note sets.

Musical set theory provides concepts for categorizing musical objects and describing their relationships. Howard Hanson first elaborated many of the concepts for analyzing tonal music. Other theorists, such as Allen Forte, further developed the theory for analyzing atonal music, drawing on the twelve-tone theory of Milton Babbitt. The concepts of musical set theory are very general and can be applied to tonal and atonal styles in any equal temperament tuning system, and to some extent more generally than that.
In music theory, a trichord is a group of three different pitch classes found within a larger group. A trichord is a contiguous three-note set from a musical scale or a twelve-tone row.
In music, the mystic chord or Prometheus chord is a six-note synthetic chord and its associated scale, or pitch collection; which loosely serves as the harmonic and melodic basis for some of the later pieces by Russian composer Alexander Scriabin. Scriabin, however, did not use the chord directly but rather derived material from its transpositions.
In music using the twelve tone technique, combinatoriality is a quality shared by twelve-tone tone rows whereby each section of a row and a proportionate number of its transformations combine to form aggregates. Much as the pitches of an aggregate created by a tone row do not need to occur simultaneously, the pitches of a combinatorially created aggregate need not occur simultaneously. Arnold Schoenberg, creator of the twelve-tone technique, often combined P-0/I-5 to create "two aggregates, between the first hexachords of each, and the second hexachords of each, respectively."

In music, a permutation (order) of a set is any ordering of the elements of that set. A specific arrangement of a set of discrete entities, or parameters, such as pitch, dynamics, or timbre. Different permutations may be related by transformation, through the application of zero or more operations, such as transposition, inversion, retrogradation, circular permutation, or multiplicative operations. These may produce reorderings of the members of the set, or may simply map the set onto itself.
Arnold Schoenberg's Piano Concerto, Op. 42 (1942) is one of his later works, written in America. It consists of four interconnected movements: Andante, Molto allegro, Adagio, and Giocoso. Around 20 minutes long, its first performance was given on February 6, 1944 at NBC Orchestra's Radio City Habitat in New York City, by Leopold Stokowski and the NBC Symphony Orchestra, with Eduard Steuermann at the piano. The first UK performance was on 7 September 1945 at the BBC Proms with Kyla Greenbaum (piano) conducted by Basil Cameron. The first German performance took place at the Darmstadt Summer School on 17 July 1948 with Peter Stadlen as the soloist.

Retrograde inversion is a musical term that literally means "backwards and upside down": "The inverse of the series is sounded in reverse order." Retrograde reverses the order of the motif's pitches: what was the first pitch becomes the last, and vice versa. This is a technique used in music, specifically in twelve-tone technique, where the inversion and retrograde techniques are performed on the same tone row successively, "[t]he inversion of the prime series in reverse order from last pitch to first."
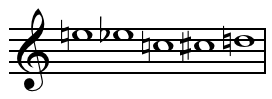
A set in music theory, as in mathematics and general parlance, is a collection of objects. In musical contexts the term is traditionally applied most often to collections of pitches or pitch-classes, but theorists have extended its use to other types of musical entities, so that one may speak of sets of durations or timbres, for example.
An all-interval tetrachord is a tetrachord, a collection of four pitch classes, containing all six interval classes. There are only two possible all-interval tetrachords, when expressed in prime form. In set theory notation, these are [0,1,4,6] (4-Z15) and [0,1,3,7] (4-Z29). Their inversions are [0,2,5,6] (4-Z15b) and [0,4,6,7] (4-Z29b). The interval vector for all all-interval tetrachords is [1,1,1,1,1,1].

A trope or tropus may refer to a variety of different concepts in medieval, 20th-, and 21st-century music.

Composition for Four Instruments (1948) is an early serial music composition written by American composer Milton Babbitt. It is Babbitt's first published ensemble work, following shortly after his Three Compositions for Piano (1947). In both these pieces, Babbitt expands upon the methods of twelve-tone composition developed by Arnold Schoenberg. He is notably innovative for his application of serial techniques to rhythm. Composition for Four Instruments is considered one of the early examples of “totally serialized” music. It is remarkable for a strong sense of integration and concentration on its particular premises—qualities that caused Elliott Carter, upon first hearing it in 1951, to persuade New Music Edition to publish it.
Fritz Heinrich Klein was an Austrian composer.
Post-tonal music theory is the set of theories put forward to describe music written outside of, or 'after', the tonal system of the common practice period. It revolves around the idea of 'emancipating dissonance', that is, freeing the structure of music from the familiar harmonic patterns that are derived from natural overtones. As music becomes more complex, dissonance becomes indistinguishable from consonance.
Anton Webern's Concerto for Nine Instruments, Op. 24, written in 1934, is a twelve-tone concerto for nine instruments: flute, oboe, clarinet, horn, trumpet, trombone, violin, viola, and piano. It consists of three movements:

In music, the all-trichord hexachord is a unique hexachord that contains all twelve trichords, or from which all twelve possible trichords may be derived. The prime form of this set class is {012478} and its Forte number is 6-Z17. Its complement is 6-Z43 and they share the interval vector of <3,2,2,3,3,2>.
The Tone Clock, and its related compositional theory Tone-Clock Theory, is a post-tonal music composition technique, developed by composers Peter Schat and Jenny McLeod. Music written using tone-clock theory features a high economy of musical intervals within a generally chromatic musical language. This is because tone-clock theory encourages the composer to generate all their harmonic and melodic material from a limited number of intervallic configurations. Tone-clock theory is also concerned with the way that the three-note pitch-class sets can be shown to underlie larger sets, and considers these triads as a fundamental unit in the harmonic world of any piece. Because there are twelve possible triadic prime forms, Schat called them the 'hours', and imagined them arrayed in a clock face, with the smallest hour in the 1 o'clock position, and the largest hour in the 12 o'clock position. A notable feature of Tone-Clock Theory is 'tone-clock steering': transposing and/or inverting hours so that each note of the chromatic aggregate is generated once and once only.