In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.

Common Lisp (CL) is a dialect of the Lisp programming language, published in American National Standards Institute (ANSI) standard document ANSI INCITS 226-1994 (S2018). The Common Lisp HyperSpec, a hyperlinked HTML version, has been derived from the ANSI Common Lisp standard.
In mathematics and computer programming, exponentiating by squaring is a general method for fast computation of large positive integer powers of a number, or more generally of an element of a semigroup, like a polynomial or a square matrix. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. These can be of quite general use, for example in modular arithmetic or powering of matrices. For semigroups for which additive notation is commonly used, like elliptic curves used in cryptography, this method is also referred to as double-and-add.

Lisp is a family of programming languages with a long history and a distinctive, fully parenthesized prefix notation. Originally specified in 1960, it is the third-oldest high-level programming language still in common use, after Fortran and COBOL. Lisp has changed since its early days, and many dialects have existed over its history. Today, the best-known general-purpose Lisp dialects are Common Lisp, Scheme, Racket, and Clojure.

Scheme is a dialect of the Lisp family of programming languages. Scheme was created during the 1970s at the MIT Computer Science and Artificial Intelligence Laboratory and released by its developers, Guy L. Steele and Gerald Jay Sussman, via a series of memos now known as the Lambda Papers. It was the first dialect of Lisp to choose lexical scope and the first to require implementations to perform tail-call optimization, giving stronger support for functional programming and associated techniques such as recursive algorithms. It was also one of the first programming languages to support first-class continuations. It had a significant influence on the effort that led to the development of Common Lisp.

Tic-tac-toe, noughts and crosses, or Xs and Os is a paper-and-pencil game for two players who take turns marking the spaces in a three-by-three grid with X or O. The player who succeeds in placing three of their marks in a horizontal, vertical, or diagonal row is the winner. It is a solved game, with a forced draw assuming best play from both players.
In computer science, a dynamic programming language is a class of high-level programming languages, which at runtime execute many common programming behaviours that static programming languages perform during compilation. These behaviors could include an extension of the program, by adding new code, by extending objects and definitions, or by modifying the type system. Although similar behaviors can be emulated in nearly any language, with varying degrees of difficulty, complexity and performance costs, dynamic languages provide direct tools to make use of them. Many of these features were first implemented as native features in the Lisp programming language.
In computer science, hygienic macros are macros whose expansion is guaranteed not to cause the accidental capture of identifiers. They are a feature of programming languages such as Scheme, Dylan, Rust, Nim, and Julia. The general problem of accidental capture was well known in the Lisp community before the introduction of hygienic macros. Macro writers would use language features that would generate unique identifiers or use obfuscated identifiers to avoid the problem. Hygienic macros are a programmatic solution to the capture problem that is integrated into the macro expander. The term "hygiene" was coined in Kohlbecker et al.'s 1986 paper that introduced hygienic macro expansion, inspired by terminology used in mathematics.
In computer science, a continuation is an abstract representation of the control state of a computer program. A continuation implements (reifies) the program control state, i.e. the continuation is a data structure that represents the computational process at a given point in the process's execution; the created data structure can be accessed by the programming language, instead of being hidden in the runtime environment. Continuations are useful for encoding other control mechanisms in programming languages such as exceptions, generators, coroutines, and so on.
In mathematics, a monomial order is a total order on the set of all (monic) monomials in a given polynomial ring, satisfying the property of respecting multiplication, i.e.,
Logic forms are simple, first-order logic knowledge representations of natural language sentences formed by the conjunction of concept predicates related through shared arguments. Each noun, verb, adjective, adverb, pronoun, preposition and conjunction generates a predicate. Logic forms can be decorated with word senses to disambiguate the semantics of the word. There are two types of predicates: events are marked with e, and entities are marked with x. The shared arguments connect the subjects and objects of verbs and prepositions together. Example input/output might look like this:
Input: The Earth provides the food we eat every day. Output: Earth:n_#1(x1) provide:v_#2(e1, x1, x2) food:n_#1(x2) we(x3) eat:v_#1(e2, x3, x2; x4) day:n_#1(x4)

The X-League is the top-level Professional Gridiron football league in Japan. It was founded in 1971 as the Japan American Football League, the first X Bowl was played in 1987. The league changed its name to the X League in 1997. There are four divisions among which there is promotion and relegation. Teams are split into different divisions or blocks, depending on the tier. There are two types of teams, one being a company team in which only employees of that particular sponsoring company may play, and the other being a club team for which anyone can try out.
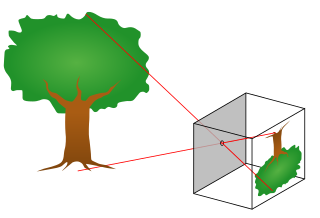
The pinhole camera model describes the mathematical relationship between the coordinates of a point in three-dimensional space and its projection onto the image plane of an ideal pinhole camera, where the camera aperture is described as a point and no lenses are used to focus light. The model does not include, for example, geometric distortions or blurring of unfocused objects caused by lenses and finite sized apertures. It also does not take into account that most practical cameras have only discrete image coordinates. This means that the pinhole camera model can only be used as a first order approximation of the mapping from a 3D scene to a 2D image. Its validity depends on the quality of the camera and, in general, decreases from the center of the image to the edges as lens distortion effects increase.
In mathematics and computer science, apply is a function that applies a function to arguments. It is central to programming languages derived from lambda calculus, such as LISP and Scheme, and also in functional languages. It has a role in the study of the denotational semantics of computer programs, because it is a continuous function on complete partial orders. Apply is also a continuous function in homotopy theory, and, indeed underpins the entire theory: it allows a homotopy deformation to be viewed as a continuous path in the space of functions. Likewise, valid mutations (refactorings) of computer programs can be seen as those that are "continuous" in the Scott topology.
The PROPT MATLAB Optimal Control Software is a new generation platform for solving applied optimal control and parameters estimation problems.
In mathematics, and more specifically in computer algebra and elimination theory, a regular chain is a particular kind of triangular set of multivariate polynomials over a field, where a triangular set is a finite sequence of polynomials such that each one contains at least one more indeterminate than the preceding one. The condition that a triangular set must satisfy to be a regular chain is that, for every k, every common zero (in an algebraically closed field) of the k first polynomials may be prolongated to a common zero of the (k + 1)th polynomial. In other words, regular chains allow solving systems of polynomial equations by solving successive univariate equations without considering different cases.
In mathematics, Boole's rule, named after George Boole, is a method of numerical integration.
LOOP is a simple register language that precisely captures the primitive recursive functions. The language is derived from the counter-machine model. Like the counter machines the LOOP language comprises a set of one or more unbounded registers, each of which can hold a single non-negative integer. A few arithmetic instructions operate on the registers. The only control flow instruction is 'LOOP x DO...END'. It causes the instructions within its scope to be repeated x times.
In mathematics, Ingleton's inequality is an inequality that is satisfied by the rank function of any representable matroid. In this sense it is a necessary condition for representability of a matroid over a finite field. Let M be a matroid and let ρ be its rank function, Ingleton's inequality states that for any subsets X1, X2, X3 and X4 in the support of M, the inequality

Lisp Flavored Erlang (LFE) is a functional, concurrent, garbage collected, general-purpose programming language and Lisp dialect built on Core Erlang and the Erlang virtual machine (BEAM). LFE builds on Erlang to provide a Lisp syntax for writing distributed, fault-tolerant, soft real-time, non-stop applications. LFE also extends Erlang to support metaprogramming with Lisp macros and an improved developer experience with a feature-rich read–eval–print loop (REPL). LFE is actively supported on all recent releases of Erlang; the oldest version of Erlang supported is R14.






