In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.

Elementary algebra encompasses the basic concepts of algebra. It is often contrasted with arithmetic: arithmetic deals with specified numbers, whilst algebra introduces variables.

Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division. The result of a multiplication operation is called a product.
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.
In elementary algebra, the quadratic formula is a formula that provides the solution(s) to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as factoring, completing the square, graphing and others.

In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind. For example, 3 × 5 is a factorization of the integer 15, and (x – 2)(x + 2) is a factorization of the polynomial x2 – 4.
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality

In algebra, a cubic equation in one variable is an equation of the form

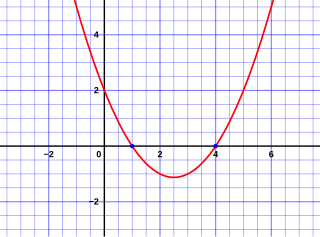
In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before the 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic".

In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the function f(x) that maps x to 1/x, is one of the simplest examples of a function which is its own inverse (an involution).

In mathematics, a quartic equation is one which can be expressed as a quartic function equaling zero. The general form of a quartic equation is

In mathematics, a quintic function is a function of the form
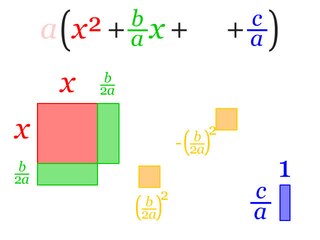
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the form

In algebra, a quartic function is a function of the form
In algebra, a binomial is a polynomial that is the sum of two terms, each of which is a monomial. It is the simplest kind of a sparse polynomial after the monomials.
In mathematics, Ruffini's rule is a method for computation of the Euclidean division of a polynomial by a binomial of the form x – r. It was described by Paolo Ruffini in 1804. The rule is a special case of synthetic division in which the divisor is a linear factor.
In mathematics, the kernel of a linear map, also known as the null space or nullspace, is the linear subspace of the domain of the map which is mapped to the zero vector. That is, given a linear map L : V → W between two vector spaces V and W, the kernel of L is the vector space of all elements v of V such that L(v) = 0, where 0 denotes the zero vector in W, or more symbolically:

In elementary algebra, a trinomial is a polynomial consisting of three terms or monomials.
In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition. Expansion of a polynomial expression can be obtained by repeatedly replacing subexpressions that multiply two other subexpressions, at least one of which is an addition, by the equivalent sum of products, continuing until the expression becomes a sum of (repeated) products. During the expansion, simplifications such as grouping of like terms or cancellations of terms may also be applied. Instead of multiplications, the expansion steps could also involve replacing powers of a sum of terms by the equivalent expression obtained from the binomial formula; this is a shortened form of what would happen if the power were treated as a repeated multiplication, and expanded repeatedly. It is customary to reintroduce powers in the final result when terms involve products of identical symbols.
























