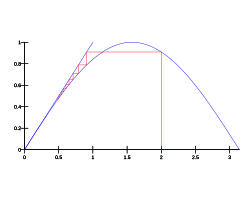
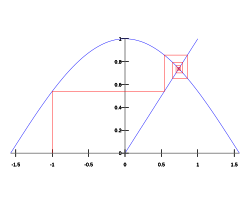
In mathematics, a contraction mapping, or contraction or contractor, on a metric space (M, d) is a function f from M to itself, with the property that there is some real number such that for all x and y in M,
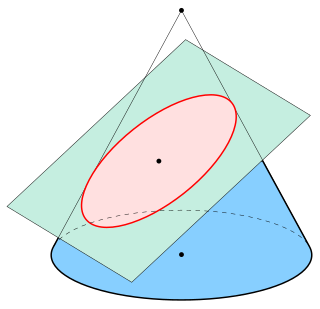
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .
In computational mathematics, an iterative method is a mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the i-th approximation is derived from the previous ones.

In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots of a real-valued function. The most basic version starts with a real-valued function f, its derivative f′, and an initial guess x0 for a root of f. If f satisfies certain assumptions and the initial guess is close, then
In mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces and provides a constructive method to find those fixed points. It can be understood as an abstract formulation of Picard's method of successive approximations. The theorem is named after Stefan Banach (1892–1945) who first stated it in 1922.
In mathematics, the radius of convergence of a power series is the radius of the largest disk at the center of the series in which the series converges. It is either a non-negative real number or . When it is positive, the power series converges absolutely and uniformly on compact sets inside the open disk of radius equal to the radius of convergence, and it is the Taylor series of the analytic function to which it converges. In case of multiple singularities of a function, the radius of convergence is the shortest or minimum of all the respective distances calculated from the center of the disk of convergence to the respective singularities of the function.
In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series is said to converge absolutely if for some real number Similarly, an improper integral of a function, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if A convergent series that is not absolutely convergent is called conditionally convergent.
In numerical analysis, a root-finding algorithm is an algorithm for finding zeros, also called "roots", of continuous functions. A zero of a function f, from the real numbers to real numbers or from the complex numbers to the complex numbers, is a number x such that f(x) = 0. As, generally, the zeros of a function cannot be computed exactly nor expressed in closed form, root-finding algorithms provide approximations to zeros, expressed either as floating-point numbers or as small isolating intervals, or disks for complex roots (an interval or disk output being equivalent to an approximate output together with an error bound).

In mathematics, a fixed point, also known as an invariant point, is a value that does not change under a given transformation. Specifically, for functions, a fixed point is an element that is mapped to itself by the function. Any set of fixed points of a transformation is also an invariant set.
In mathematics, specifically the study of differential equations, the Picard–Lindelöf theorem gives a set of conditions under which an initial value problem has a unique solution. It is also known as Picard's existence theorem, the Cauchy–Lipschitz theorem, or the existence and uniqueness theorem.
In mathematical analysis, particularly numerical analysis, the rate of convergence and order of convergence of a sequence that converges to a limit are any of several characterizations of how quickly that sequence approaches its limit. These are broadly divided into rates and orders of convergence that describe how quickly a sequence further approaches its limit once it is already close to it, called asymptotic rates and orders of convergence, and those that describe how quickly sequences approach their limits from starting points that are not necessarily close to their limits, called non-asymptotic rates and orders of convergence.

In mathematics, an iterated function is a function that is obtained by composing another function with itself two or several times. The process of repeatedly applying the same function is called iteration. In this process, starting from some initial object, the result of applying a given function is fed again into the function as input, and this process is repeated.
In the mathematical field of analysis, the Nash–Moser theorem, discovered by mathematician John Forbes Nash and named for him and Jürgen Moser, is a generalization of the inverse function theorem on Banach spaces to settings when the required solution mapping for the linearized problem is not bounded.

In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle, and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle , the sine and cosine functions are denoted as and .
Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations.
The Kantorovich theorem, or Newton–Kantorovich theorem, is a mathematical statement on the semi-local convergence of Newton's method. It was first stated by Leonid Kantorovich in 1948. It is similar to the form of the Banach fixed-point theorem, although it states existence and uniqueness of a zero rather than a fixed point.
In mathematics, for a sequence of complex numbers a1, a2, a3, ... the infinite product
In mathematics, infinite compositions of analytic functions (ICAF) offer alternative formulations of analytic continued fractions, series, products and other infinite expansions, and the theory evolving from such compositions may shed light on the convergence/divergence of these expansions. Some functions can actually be expanded directly as infinite compositions. In addition, it is possible to use ICAF to evaluate solutions of fixed point equations involving infinite expansions. Complex dynamics offers another venue for iteration of systems of functions rather than a single function. For infinite compositions of a single function see Iterated function. For compositions of a finite number of functions, useful in fractal theory, see Iterated function system.

In mathematics, the Dottie number is a constant that is the unique real root of the equation
Convergence proof techniques are canonical patterns of mathematical proofs that sequences or functions converge to a finite limit when the argument tends to infinity.