
Geodesy or geodetics is the science of measuring and representing the geometry, gravity, and spatial orientation of the Earth in temporally varying 3D. It is called planetary geodesy when studying other astronomical bodies, such as planets or circumplanetary systems. Geodesy is an earth science and many consider the study of Earth's shape and gravity to be central to that science. It is also a discipline of applied mathematics.

In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three real numbers: the radial distancer along the radial line connecting the point to the fixed point of origin; the polar angleθ between the radial line and a polar axis; and the azimuthal angleφ as the angle of rotation of the radial line around the polar axis. (See graphic re the "physics convention".) Once the radius is fixed, the three coordinates (r, θ, φ), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates.
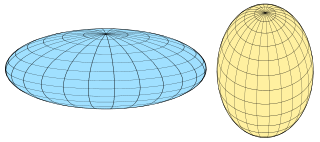
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.
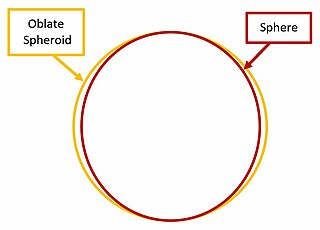
An equatorial bulge is a difference between the equatorial and polar diameters of a planet, due to the centrifugal force exerted by the rotation about the body's axis. A rotating body tends to form an oblate spheroid rather than a sphere.
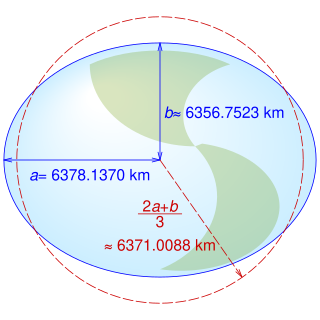
Earth radius is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) to a minimum of nearly 6,357 km (3,950 mi).
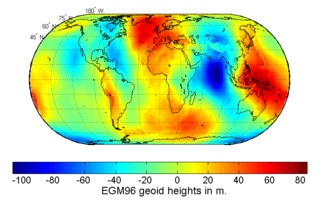
The geoid is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth's rotation, if other influences such as winds and tides were absent. This surface is extended through the continents. According to Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but irregular surface whose shape results from the uneven distribution of mass within and on the surface of Earth. It can be known only through extensive gravitational measurements and calculations. Despite being an important concept for almost 200 years in the history of geodesy and geophysics, it has been defined to high precision only since advances in satellite geodesy in the late 20th century.
Geopotential is the potential of the Earth's gravity field. For convenience it is often defined as the negative of the potential energy per unit mass, so that the gravity vector is obtained as the gradient of the geopotential, without the negation. In addition to the actual potential, a theoretical normal potential and their difference, the disturbing potential, can also be defined.

The World Geodetic System (WGS) is a standard used in cartography, geodesy, and satellite navigation including GPS. The current version, WGS 84, defines an Earth-centered, Earth-fixed coordinate system and a geodetic datum, and also describes the associated Earth Gravitational Model (EGM) and World Magnetic Model (WMM). The standard is published and maintained by the United States National Geospatial-Intelligence Agency.

In geodesy, the figure of the Earth is the size and shape used to model planet Earth. The kind of figure depends on application, including the precision needed for the model. A spherical Earth is a well-known historical approximation that is satisfactory for geography, astronomy and many other purposes. Several models with greater accuracy have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns.
In geodesy, conversion among different geographic coordinate systems is made necessary by the different geographic coordinate systems in use across the world and over time. Coordinate conversion is composed of a number of different types of conversion: format change of geographic coordinates, conversion of coordinate systems, or transformation to different geodetic datums. Geographic coordinate conversion has applications in cartography, surveying, navigation and geographic information systems.

A geodetic datum or geodetic system is a global datum reference or reference frame for unambiguously representing the position of locations on Earth by means of either geodetic coordinates or geocentric coordinates. Datums are crucial to any technology or technique based on spatial location, including geodesy, navigation, surveying, geographic information systems, remote sensing, and cartography. A horizontal datum is used to measure a horizontal position, across the Earth's surface, in latitude and longitude or another related coordinate system. A vertical datum is used to measure the elevation or depth relative to a standard origin, such as mean sea level (MSL). A three-dimensional datum enables the expression of both horizontal and vertical position components in a unified form. The concept can be generalized for other celestial bodies as in planetary datums.
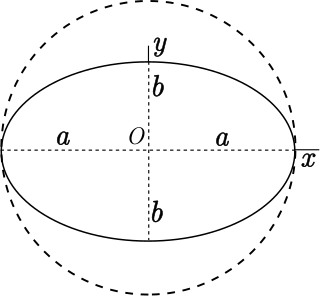
Flattening is a measure of the compression of a circle or sphere along a diameter to form an ellipse or an ellipsoid of revolution (spheroid) respectively. Other terms used are ellipticity, or oblateness. The usual notation for flattening is and its definition in terms of the semi-axes and of the resulting ellipse or ellipsoid is
In geodesy and navigation, a meridian arc is the curve between two points on the Earth's surface having the same longitude. The term may refer either to a segment of the meridian, or to its length.
An Earth ellipsoid or Earth spheroid is a mathematical figure approximating the Earth's form, used as a reference frame for computations in geodesy, astronomy, and the geosciences. Various different ellipsoids have been used as approximations.

Geodetic coordinates are a type of curvilinear orthogonal coordinate system used in geodesy based on a reference ellipsoid. They include geodetic latitude (north/south) ϕ, longitude (east/west) λ, and ellipsoidal heighth. The triad is also known as Earth ellipsoidal coordinates.
In geodesy and geophysics, theoretical gravity or normal gravity is an approximation of the true gravity on Earth's surface by means of a mathematical model representing Earth. The most common model of a smoothed Earth is a rotating Earth ellipsoid of revolution.

The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an oblate ellipsoid, a slightly flattened sphere. A geodesic is the shortest path between two points on a curved surface, analogous to a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry.

Web Mercator, Google Web Mercator, Spherical Mercator, WGS 84 Web Mercator or WGS 84/Pseudo-Mercator is a variant of the Mercator map projection and is the de facto standard for Web mapping applications. It rose to prominence when Google Maps adopted it in 2005. It is used by virtually all major online map providers, including Google Maps, CARTO, Mapbox, Bing Maps, OpenStreetMap, Mapquest, Esri, and many others. Its official EPSG identifier is EPSG:3857, although others have been used historically.

A planetary coordinate system is a generalization of the geographic, geodetic, and the geocentric coordinate systems for planets other than Earth. Similar coordinate systems are defined for other solid celestial bodies, such as in the selenographic coordinates for the Moon. The coordinate systems for almost all of the solid bodies in the Solar System were established by Merton E. Davies of the Rand Corporation, including Mercury, Venus, Mars, the four Galilean moons of Jupiter, and Triton, the largest moon of Neptune. A planetary datum is a generalization of geodetic datums for other planetary bodies, such as the Mars datum; it requires the specification of physical reference points or surfaces with fixed coordinates, such as a specific crater for the reference meridian or the best-fitting equigeopotential as zero-level surface.









































