| Geodesy |
|---|
 |
The World Geodetic System (WGS) is a standard used in cartography, geodesy, and satellite navigation including GPS. The current version, WGS 84, defines an Earth-centered, Earth-fixed coordinate system and a geodetic datum, and also describes the associated Earth Gravitational Model (EGM) and World Magnetic Model (WMM). The standard is published and maintained by the United States National Geospatial-Intelligence Agency. [1]
Efforts to supplement the various national surveying systems began in the 19th century with F.R. Helmert's book Mathematische und Physikalische Theorien der Physikalischen Geodäsie (Mathematical and Physical Theories of Physical Geodesy). Austria and Germany founded the Zentralbüro für die Internationale Erdmessung (Central Bureau of International Geodesy), and a series of global ellipsoids of the Earth were derived (e.g., Helmert 1906, Hayford 1910 and 1924).
A unified geodetic system for the whole world became essential in the 1950s for several reasons:
In the late 1950s, the United States Department of Defense, together with scientists of other institutions and countries, began to develop the needed world system to which geodetic data could be referred and compatibility established between the coordinates of widely separated sites of interest. Efforts of the U.S. Army, Navy and Air Force were combined leading to the DoD World Geodetic System 1960 (WGS 60). The term datum as used here refers to a smooth surface somewhat arbitrarily defined as zero elevation, consistent with a set of surveyor's measures of distances between various stations, and differences in elevation, all reduced to a grid of latitudes, longitudes, and elevations. Heritage surveying methods found elevation differences from a local horizontal determined by the spirit level, plumb line, or an equivalent device that depends on the local gravity field (see physical geodesy). As a result, the elevations in the data are referenced to the geoid, a surface that is not readily found using satellite geodesy. The latter observational method is more suitable for global mapping. Therefore, a motivation, and a substantial problem in the WGS and similar work is to patch together data that were not only made separately, for different regions, but to re-reference the elevations to an ellipsoid model rather than to the geoid.
In accomplishing WGS 60, a combination of available surface gravity data, astro-geodetic data and results from HIRAN [2] and Canadian SHORAN surveys were used to define a best-fitting ellipsoid and an earth-centered orientation for each initially selected datum. (Every datum is relatively oriented with respect to different portions of the geoid by the astro-geodetic methods already described.) The sole contribution of satellite data to the development of WGS 60 was a value for the ellipsoid flattening which was obtained from the nodal motion of a satellite.
Prior to WGS 60, the U.S. Army and U.S. Air Force had each developed a world system by using different approaches to the gravimetric datum orientation method. To determine their gravimetric orientation parameters, the Air Force used the mean of the differences between the gravimetric and astro-geodetic deflections and geoid heights (undulations) at specifically selected stations in the areas of the major datums. The Army performed an adjustment to minimize the difference between astro-geodetic and gravimetric geoids. By matching the relative astro-geodetic geoids of the selected datums with an earth-centered gravimetric geoid, the selected datums were reduced to an earth-centered orientation. Since the Army and Air Force systems agreed remarkably well for the NAD, ED and TD areas, they were consolidated and became WGS 60.
Improvements to the global system included the Astrogeoid of Irene Fischer and the astronautic Mercury datum. In January 1966, a World Geodetic System Committee composed of representatives from the United States Army, Navy and Air Force was charged with developing an improved WGS, needed to satisfy mapping, charting and geodetic requirements. Additional surface gravity observations, results from the extension of triangulation and trilateration networks, and large amounts of Doppler and optical satellite data had become available since the development of WGS 60. Using the additional data and improved techniques, WGS 66 was produced which served DoD needs for about five years after its implementation in 1967. The defining parameters of the WGS 66 Ellipsoid were the flattening (1⁄298.25 determined from satellite data) and the semimajor axis (6378145 m determined from a combination of Doppler satellite and astro-geodetic data). A worldwide 5° × 5° mean free air gravity anomaly field provided the basic data for producing the WGS 66 gravimetric geoid. Also, a geoid referenced to the WGS 66 Ellipsoid was derived from available astrogeodetic data to provide a detailed representation of limited land areas.
After an extensive effort over a period of approximately three years, the Department of Defense World Geodetic System 1972 was completed. Selected satellite, surface gravity and astrogeodetic data available through 1972 from both DoD and non-DoD sources were used in a Unified WGS Solution (a large scale least squares adjustment). The results of the adjustment consisted of corrections to initial station coordinates and coefficients of the gravitational field. [3]
The largest collection of data ever used for WGS purposes was assembled, processed and applied in the development of WGS 72. Both optical and electronic satellite data were used. The electronic satellite data consisted, in part, of Doppler data provided by the U.S. Navy and cooperating non-DoD satellite tracking stations established in support of the Navy's Navigational Satellite System (NNSS). Doppler data was also available from the numerous sites established by GEOCEIVERS during 1971 and 1972. Doppler data was the primary data source for WGS 72 (see image). Additional electronic satellite data was provided by the SECOR (Sequential Collation of Range) Equatorial Network completed by the U.S. Army in 1970. Optical satellite data from the Worldwide Geometric Satellite Triangulation Program was provided by the BC-4 camera system (see image). Data from the Smithsonian Astrophysical Observatory was also used which included camera (Baker–Nunn) and some laser ranging. [3]
The surface gravity field used in the Unified WGS Solution consisted of a set of 410 10° × 10° equal area mean free air gravity anomalies determined solely from terrestrial data. This gravity field includes mean anomaly values compiled directly from observed gravity data wherever the latter was available in sufficient quantity. The value for areas of sparse or no observational data were developed from geophysically compatible gravity approximations using gravity-geophysical correlation techniques. Approximately 45 percent of the 410 mean free air gravity anomaly values were determined directly from observed gravity data. [3]
The astrogeodetic data in its basic form consists of deflection of the vertical components referred to the various national geodetic datums. These deflection values were integrated into astrogeodetic geoid charts referred to these national datums. The geoid heights contributed to the Unified WGS Solution by providing additional and more detailed data for land areas. Conventional ground survey data was included in the solution to enforce a consistent adjustment of the coordinates of neighboring observation sites of the BC-4, SECOR, Doppler and Baker–Nunn systems. Also, eight geodimeter long line precise traverses were included for the purpose of controlling the scale of the solution. [3]
The Unified WGS Solution, as stated above, was a solution for geodetic positions and associated parameters of the gravitational field based on an optimum combination of available data. The WGS 72 ellipsoid parameters, datum shifts and other associated constants were derived separately. For the unified solution, a normal equation matrix was formed based on each of the mentioned data sets. Then, the individual normal equation matrices were combined and the resultant matrix solved to obtain the positions and the parameters. [3]
The value for the semimajor axis (a) of the WGS 72 Ellipsoid is 6378135 m. The adoption of an a-value 10 meters smaller than that for the WGS 66 Ellipsoid was based on several calculations and indicators including a combination of satellite and surface gravity data for position and gravitational field determinations. Sets of satellite derived station coordinates and gravimetric deflection of the vertical and geoid height data were used to determine local-to-geocentric datum shifts, datum rotation parameters, a datum scale parameter and a value for the semimajor axis of the WGS Ellipsoid. Eight solutions were made with the various sets of input data, both from an investigative point of view and also because of the limited number of unknowns which could be solved for in any individual solution due to computer limitations. Selected Doppler satellite tracking and astro-geodetic datum orientation stations were included in the various solutions. Based on these results and other related studies accomplished by the committee, an a-value of 6378135 m and a flattening of 1/298.26 were adopted. [3]
In the development of local-to WGS 72 datum shifts, results from different geodetic disciplines were investigated, analyzed and compared. Those shifts adopted were based primarily on a large number of Doppler TRANET and GEOCEIVER station coordinates which were available worldwide. These coordinates had been determined using the Doppler point positioning method. [3]
In the early 1980s, the need for a new world geodetic system was generally recognized by the geodetic community as well as within the US Department of Defense. WGS 72 no longer provided sufficient data, information, geographic coverage, or product accuracy for all then-current and anticipated applications. The means for producing a new WGS were available in the form of improved data, increased data coverage, new data types and improved techniques. Observations from Doppler, satellite laser ranging and very-long-baseline interferometry (VLBI) constituted significant new information. An outstanding new source of data had become available from satellite radar altimetry. Also available was an advanced least squares method called collocation that allowed for a consistent combination solution from different types of measurements all relative to the Earth's gravity field, measurements such as the geoid, gravity anomalies, deflections, and dynamic Doppler.
The new world geodetic system was called WGS 84. It is the reference system used by the Global Positioning System. It is geocentric and globally consistent within 1 m . Current geodetic realizations of the geocentric reference system family International Terrestrial Reference System (ITRS) maintained by the IERS are geocentric, and internally consistent, at the few-cm level, while still being metre-level consistent with WGS 84.
The WGS 84 reference ellipsoid was based on GRS 80, but it contains a very slight variation in the inverse flattening, as it was derived independently and the result was rounded to a different number of significant digits. [4] This resulted in a tiny difference of 0.105 mm in the semi-minor axis. [5] The following table compares the primary ellipsoid parameters.
| Ellipsoid reference | Semi-major axis a | Semi-minor axis b | Inverse flattening 1⁄f |
|---|---|---|---|
| GRS 80 | 6378137.0 m | ≈ 6356752.314140 m | 298.257222100882711... |
| WGS 84 [6] | 6378137.0 m | ≈ 6356752.314245 m | 298.257223563 |
The coordinate origin of WGS 84 is meant to be located at the Earth's center of mass; the uncertainty is believed to be less than 2 cm. [7]
The WGS 84 meridian of zero longitude is the IERS Reference Meridian, [8] 5.3 arc seconds or 102 metres (335 ft) east of the Greenwich meridian at the latitude of the Royal Observatory. [9] [10] (This is related to the fact that the local gravity field at Greenwich does not point exactly through the Earth's center of mass, but rather "misses west" of the center of mass by about 102 meters.) The longitude positions on WGS 84 agree with those on the older North American Datum 1927 at roughly 85° longitude west, in the east-central United States.
The WGS 84 datum surface is an oblate spheroid with equatorial radius a = 6378137 m at the equator and flattening f = 1⁄298.257223563. The refined value of the WGS 84 gravitational constant (mass of Earth's atmosphere included) is GM = 3.986004418×1014 m3/s2. The angular velocity of the Earth is defined to be ω = 72.92115×10−6 rad/s. [11]
This leads to several computed parameters such as the polar semi-minor axis b which equals a × (1 − f) = 6356752.3142 m, and the first eccentricity squared, e2 = 6.69437999014×10−3. [11]
The original standardization document for WGS 84 was Technical Report 8350.2, published in September 1987 by the Defense Mapping Agency (which later became the National Imagery and Mapping Agency). New editions were published in September 1991 and July 1997; the latter edition was amended twice, in January 2000 and June 2004. [12] The standardization document was revised again and published in July 2014 by the National Geospatial-Intelligence Agency as NGA.STND.0036. [13] These updates provide refined descriptions of the Earth and realizations of the system for higher precision.
The original WGS84 model had an absolute accuracy of 1–2 meters. WGS84 (G730) first incorporated GPS observations, taking the accuracy down to 10 cm/component rms. [14] All following revisions including WGS84 (G873) and WGS84 (G1150) also used GPS. [15]
WGS 84 (G1762) is the sixth update to the WGS reference frame. [14]
WGS 84 has most recently been updated to use the reference frame G2296, which was released on 7 January 2024 as an update to G2139, now aligned to both the ITRF2020, the most recent ITRF realization, and the IGS20, the frame used by the International GNSS Service (IGS). [16] G2139 was aligned with the IGb14 realization of the International Terrestrial Reference Frame (ITRF) 2014 and uses the new IGS Antex standard. [17]
Updates to the original geoid for WGS 84 are now published as a separate Earth Gravitational Model (EGM), with improved resolution and accuracy. Likewise, the World Magnetic Model (WMM) is updated separately. The current version of WGS 84 uses EGM2008 and WMM2020. [18] [19]
Solution for Earth orientation parameters consistent with ITRF2014 is also needed (IERS EOP 14C04). [20]
Components of WGS 84 are identified by codes in the EPSG Geodetic Parameter Dataset: [21]
Geodesy or geodetics is the science of measuring and representing the geometry, gravity, and spatial orientation of the Earth in temporally varying 3D. It is called planetary geodesy when studying other astronomical bodies, such as planets or circumplanetary systems. Geodesy is an earth science and many consider the study of Earth's shape and gravity to be central to that science. It is also a discipline of applied mathematics.
In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.
A geographic coordinate system (GCS) is a spherical or geodetic coordinate system for measuring and communicating positions directly on Earth as latitude and longitude. It is the simplest, oldest and most widely used type of the various spatial reference systems that are in use, and forms the basis for most others. Although latitude and longitude form a coordinate tuple like a cartesian coordinate system, the geographic coordinate system is not cartesian because the measurements are angles and are not on a planar surface.
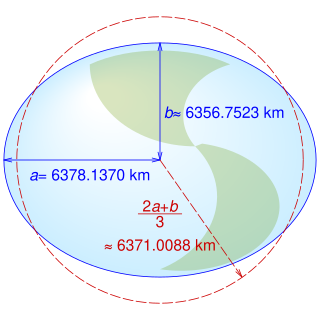
Earth radius is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) to a minimum of nearly 6,357 km (3,950 mi).
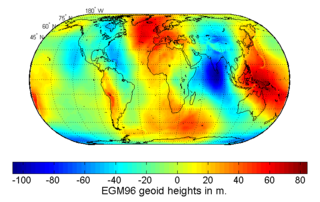
The geoid is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth's rotation, if other influences such as winds and tides were absent. This surface is extended through the continents. According to Carl Friedrich Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but irregular surface whose shape results from the uneven distribution of mass within and on the surface of Earth. It can be known only through extensive gravitational measurements and calculations. Despite being an important concept for almost 200 years in the history of geodesy and geophysics, it has been defined to high precision only since advances in satellite geodesy in the late 20th century.
In geodesy, the figure of the Earth is the size and shape used to model planet Earth. The kind of figure depends on application, including the precision needed for the model. A spherical Earth is a well-known historical approximation that is satisfactory for geography, astronomy and many other purposes. Several models with greater accuracy have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns.
The Geodetic Reference System 1980 (GRS80) consists of a global reference ellipsoid and a normal gravity model. The GRS80 gravity model has been followed by the newer more accurate Earth Gravitational Models, but the GRS80 reference ellipsoid is still the most accurate in use for coordinate reference systems, e.g. for the international ITRS, the European ETRS89 and for WGS 84 used for the American Global Navigation Satellite System (GPS).
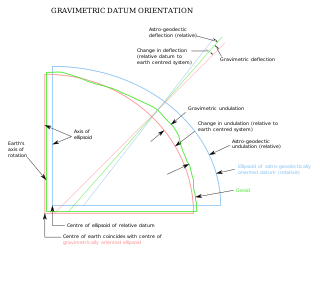
The vertical deflection (VD) or deflection of the vertical (DoV), also known as deflection of the plumb line and astro-geodetic deflection, is a measure of how far the gravity direction at a given point of interest is rotated by local mass anomalies such as nearby mountains. They are widely used in geodesy, for surveying networks and for geophysical purposes.
A geodetic datum or geodetic system is a global datum reference or reference frame for unambiguously representing the position of locations on Earth by means of either geodetic coordinates or geocentric coordinates. Datums are crucial to any technology or technique based on spatial location, including geodesy, navigation, surveying, geographic information systems, remote sensing, and cartography. A horizontal datum is used to measure a horizontal position, across the Earth's surface, in latitude and longitude or another related coordinate system. A vertical datum is used to measure the elevation or depth relative to a standard origin, such as mean sea level (MSL). A three-dimensional datum enables the expression of both horizontal and vertical position components in a unified form. The concept can be generalized for other celestial bodies as in planetary datums.
Satellite geodesy is geodesy by means of artificial satellites—the measurement of the form and dimensions of Earth, the location of objects on its surface and the figure of the Earth's gravity field by means of artificial satellite techniques. It belongs to the broader field of space geodesy. Traditional astronomical geodesy is not commonly considered a part of satellite geodesy, although there is considerable overlap between the techniques.
ED50 is a geodetic datum which was defined after World War II for the international connection of geodetic networks.
A spatial reference system (SRS) or coordinate reference system (CRS) is a framework used to precisely measure locations on the surface of Earth as coordinates. It is thus the application of the abstract mathematics of coordinate systems and analytic geometry to geographic space. A particular SRS specification comprises a choice of Earth ellipsoid, horizontal datum, map projection, origin point, and unit of measure. Thousands of coordinate systems have been specified for use around the world or in specific regions and for various purposes, necessitating transformations between different SRS.
The North American Datum (NAD) is the horizontal datum now used to define the geodetic network in North America. A datum is a formal description of the shape of the Earth along with an "anchor" point for the coordinate system. In surveying, cartography, and land-use planning, two North American Datums are in use for making lateral or "horizontal" measurements: the North American Datum of 1927 (NAD 27) and the North American Datum of 1983 (NAD 83). Both are geodetic reference systems based on slightly different assumptions and measurements.
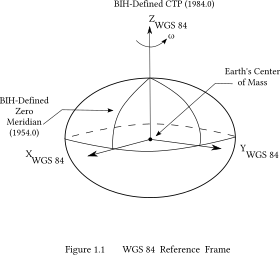
The Earth-centered, Earth-fixed coordinate system, also known as the geocentric coordinate system, is a cartesian spatial reference system that represents locations in the vicinity of the Earth as X, Y, and Z measurements from its center of mass. Its most common use is in tracking the orbits of satellites and in satellite navigation systems for measuring locations on the surface of the Earth, but it is also used in applications such as tracking crustal motion.
The Earth Gravitational Models (EGM) are a series of geopotential models of the Earth published by the National Geospatial-Intelligence Agency (NGA). They are used as the geoid reference in the World Geodetic System.
The North American Vertical Datum of 1988 is the vertical datum for orthometric heights established for vertical control surveying in the United States based upon the General Adjustment of the North American Datum of 1988.
The Bessel ellipsoid is an important reference ellipsoid of geodesy. It is currently used by several countries for their national geodetic surveys, but will be replaced in the next decades by modern ellipsoids of satellite geodesy.
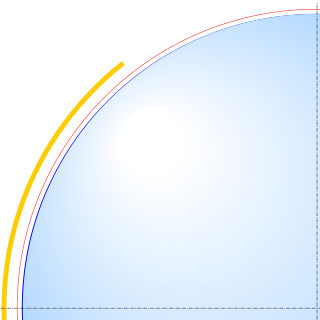
An Earth ellipsoid or Earth spheroid is a mathematical figure approximating the Earth's form, used as a reference frame for computations in geodesy, astronomy, and the geosciences. Various different ellipsoids have been used as approximations.
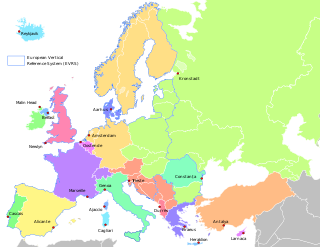
In geodesy, surveying, hydrography and navigation, vertical datum or altimetric datum is a reference coordinate surface used for vertical positions, such as the elevations of Earth-bound features and altitudes of satellite orbits and in aviation. In planetary science, vertical datums are also known as zero-elevation surface or zero-level reference.
Web Mercator, Google Web Mercator, Spherical Mercator, WGS 84 Web Mercator or WGS 84/Pseudo-Mercator is a variant of the Mercator map projection and is the de facto standard for Web mapping applications. It rose to prominence when Google Maps adopted it in 2005. It is used by virtually all major online map providers, including Google Maps, CARTO, Mapbox, Bing Maps, OpenStreetMap, Mapquest, Esri, and many others. Its official EPSG identifier is EPSG:3857, although others have been used historically.
This article incorporates public domain material from websites or documents of the National Geodetic Survey .
