The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In fluid dynamics, potential flow or irrotational flow refers to a description of a fluid flow with no vorticity in it. Such a description typically arises in the limit of vanishing viscosity, i.e., for an inviscid fluid and with no vorticity present in the flow.
The vorticity equation of fluid dynamics describes the evolution of the vorticity ω of a particle of a fluid as it moves with its flow; that is, the local rotation of the fluid. The governing equation is:

In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a no-slip boundary condition. The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer.
In atmospheric science, geostrophic flow is the theoretical wind that would result from an exact balance between the Coriolis force and the pressure gradient force. This condition is called geostrophic equilibrium or geostrophic balance. The geostrophic wind is directed parallel to isobars. This balance seldom holds exactly in nature. The true wind almost always differs from the geostrophic wind due to other forces such as friction from the ground. Thus, the actual wind would equal the geostrophic wind only if there were no friction and the isobars were perfectly straight. Despite this, much of the atmosphere outside the tropics is close to geostrophic flow much of the time and it is a valuable first approximation. Geostrophic flow in air or water is a zero-frequency inertial wave.

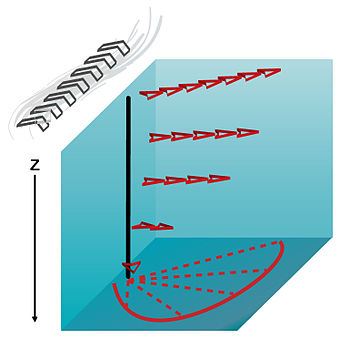
The Ekman spiral is an arrangement of ocean currents: the directions of horizontal current appear to twist as the depth changes. The oceanic wind driven Ekman spiral is the result of a force balance created by a shear stress force, Coriolis force and the water drag. This force balance gives a resulting current of the water different from the winds. In the ocean, there are two places where the Ekman spiral can be observed. At the surface of the ocean, the shear stress force corresponds with the wind stress force. At the bottom of the ocean, the shear stress force is created by friction with the ocean floor. This phenomenon was first observed at the surface by the Norwegian oceanographer Fridtjof Nansen during his Fram expedition. He noticed that icebergs did not drift in the same direction as the wind. His student, the Swedish oceanographer Vagn Walfrid Ekman, was the first person to physically explain this process.
The Sverdrup balance, or Sverdrup relation, is a theoretical relationship between the wind stress exerted on the surface of the open ocean and the vertically integrated meridional (north-south) transport of ocean water.
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.

Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.

Ekman transport is part of Ekman motion theory, first investigated in 1902 by Vagn Walfrid Ekman. Winds are the main source of energy for ocean circulation, and Ekman transport is a component of wind-driven ocean current. Ekman transport occurs when ocean surface waters are influenced by the friction force acting on them via the wind. As the wind blows it casts a friction force on the ocean surface that drags the upper 10-100m of the water column with it. However, due to the influence of the Coriolis effect, the ocean water moves at a 90° angle from the direction of the surface wind. The direction of transport is dependent on the hemisphere: in the northern hemisphere, transport occurs at 90° clockwise from wind direction, while in the southern hemisphere it occurs at 90° anticlockwise. This phenomenon was first noted by Fridtjof Nansen, who recorded that ice transport appeared to occur at an angle to the wind direction during his Arctic expedition of the 1890s. Ekman transport has significant impacts on the biogeochemical properties of the world's oceans. This is because it leads to upwelling and downwelling in order to obey mass conservation laws. Mass conservation, in reference to Ekman transfer, requires that any water displaced within an area must be replenished. This can be done by either Ekman suction or Ekman pumping depending on wind patterns.
The derivation of the Navier–Stokes equations as well as their application and formulation for different families of fluids, is an important exercise in fluid dynamics with applications in mechanical engineering, physics, chemistry, heat transfer, and electrical engineering. A proof explaining the properties and bounds of the equations, such as Navier–Stokes existence and smoothness, is one of the important unsolved problems in mathematics.
In physical oceanography and fluid dynamics, the wind stress is the shear stress exerted by the wind on the surface of large bodies of water – such as oceans, seas, estuaries and lakes. When wind is blowing over a water surface, the wind applies a wind force on the water surface. The wind stress is the component of this wind force that is parallel to the surface per unit area. Also, the wind stress can be described as the flux of horizontal momentum applied by the wind on the water surface. The wind stress causes a deformation of the water body whereby wind waves are generated. Also, the wind stress drives ocean currents and is therefore an important driver of the large-scale ocean circulation. The wind stress is affected by the wind speed, the shape of the wind waves and the atmospheric stratification. It is one of the components of the air–sea interaction, with others being the atmospheric pressure on the water surface, as well as the exchange of energy and mass between the water and the atmosphere.
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.
Shear velocity, also called friction velocity, is a form by which a shear stress may be re-written in units of velocity. It is useful as a method in fluid mechanics to compare true velocities, such as the velocity of a flow in a stream, to a velocity that relates shear between layers of flow.
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.
Ocean dynamics define and describe the flow of water within the oceans. Ocean temperature and motion fields can be separated into three distinct layers: mixed (surface) layer, upper ocean, and deep ocean.

In fluid dynamics, the radiation stress is the depth-integrated – and thereafter phase-averaged – excess momentum flux caused by the presence of the surface gravity waves, which is exerted on the mean flow. The radiation stresses behave as a second-order tensor.
In oceanography, Ekman velocity – also referred as a kind of the residual ageostrophic velocity as it deviates from geostrophy – is part of the total horizontal velocity (u) in the upper layer of water of the open ocean. This velocity, caused by winds blowing over the surface of the ocean, is such that the Coriolis force on this layer is balanced by the force of the wind.
In physical oceanography and fluid mechanics, the Miles-Phillips mechanism describes the generation of wind waves from a flat sea surface by two distinct mechanisms. Wind blowing over the surface generates tiny wavelets. These wavelets develop over time and become ocean surface waves by absorbing the energy transferred from the wind. The Miles-Phillips mechanism is a physical interpretation of these wind-generated surface waves.
Both mechanisms are applied to gravity-capillary waves and have in common that waves are generated by a resonance phenomenon. The Miles mechanism is based on the hypothesis that waves arise as an instability of the sea-atmosphere system. The Phillips mechanism assumes that turbulent eddies in the atmospheric boundary layer induce pressure fluctuations at the sea surface. The Phillips mechanism is generally assumed to be important in the first stages of wave growth, whereas the Miles mechanism is important in later stages where the wave growth becomes exponential in time.
The recharge oscillator model for El Niño–Southern Oscillation (ENSO) is a theory described for the first time in 1997 by Jin., which explains the periodical variation of the sea surface temperature (SST) and thermocline depth that occurs in the central equatorial Pacific Ocean. The physical mechanisms at the basis of this oscillation are periodical recharges and discharges of the zonal mean equatorial heat content, due to ocean-atmosphere interaction. Other theories have been proposed to model ENSO, such as the delayed oscillator, the western Pacific oscillator and the advective reflective oscillator. A unified and consistent model has been proposed by Wang in 2001, in which the recharge oscillator model is included as a particular case.