
In mathematics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.

In physics, the Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
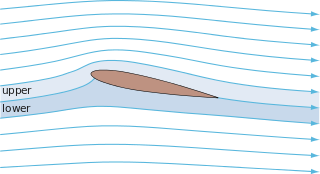
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the curl of the gradient of a scalar always being equal to zero.

In fluid dynamics, gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere and the ocean, which gives rise to wind waves.
The primitive equations are a set of nonlinear partial differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations:
- A continuity equation: Representing the conservation of mass.
- Conservation of momentum: Consisting of a form of the Navier–Stokes equations that describe hydrodynamical flow on the surface of a sphere under the assumption that vertical motion is much smaller than horizontal motion (hydrostasis) and that the fluid layer depth is small compared to the radius of the sphere
- A thermal energy equation: Relating the overall temperature of the system to heat sources and sinks
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.

The shallow-water equations (SWE) are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid. The shallow-water equations in unidirectional form are also called Saint-Venant equations, after Adhémar Jean Claude Barré de Saint-Venant.
Atmospheric tides are global-scale periodic oscillations of the atmosphere. In many ways they are analogous to ocean tides. Atmospheric tides can be excited by:

For a pure wave motion in fluid dynamics, the Stokes drift velocity is the average velocity when following a specific fluid parcel as it travels with the fluid flow. For instance, a particle floating at the free surface of water waves, experiences a net Stokes drift velocity in the direction of wave propagation.

In fluid dynamics, a Stokes wave is a nonlinear and periodic surface wave on an inviscid fluid layer of constant mean depth. This type of modelling has its origins in the mid 19th century when Sir George Stokes – using a perturbation series approach, now known as the Stokes expansion – obtained approximate solutions for nonlinear wave motion.
The omega equation is a culminating result in synoptic-scale meteorology. It is an elliptic partial differential equation, named because its left-hand side produces an estimate of vertical velocity, customarily expressed by symbol , in a pressure coordinate measuring height the atmosphere. Mathematically, , where represents a material derivative. The underlying concept is more general, however, and can also be applied to the Boussinesq fluid equation system where vertical velocity is in altitude coordinate z.
In fluid dynamics, Luke's variational principle is a Lagrangian variational description of the motion of surface waves on a fluid with a free surface, under the action of gravity. This principle is named after J.C. Luke, who published it in 1967. This variational principle is for incompressible and inviscid potential flows, and is used to derive approximate wave models like the mild-slope equation, or using the averaged Lagrangian approach for wave propagation in inhomogeneous media.
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
Equatorial Rossby waves, often called planetary waves, are very long, low frequency water waves found near the equator and are derived using the equatorial beta plane approximation.

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.

In fluid dynamics, the radiation stress is the depth-integrated – and thereafter phase-averaged – excess momentum flux caused by the presence of the surface gravity waves, which is exerted on the mean flow. The radiation stresses behave as a second-order tensor.

In fluid dynamics, Green's law, named for 19th-century British mathematician George Green, is a conservation law describing the evolution of non-breaking, surface gravity waves propagating in shallow water of gradually varying depth and width. In its simplest form, for wavefronts and depth contours parallel to each other, it states:
The Sack–Schamel equation describes the nonlinear evolution of the cold ion fluid in a two-component plasma under the influence of a self-organized electric field. It is a partial differential equation of second order in time and space formulated in Lagrangian coordinates. The dynamics described by the equation take place on an ionic time scale, which allows electrons to be treated as if they were in equilibrium and described by an isothermal Boltzmann distribution. Supplemented by suitable boundary conditions, it describes the entire configuration space of possible events the ion fluid is capable of, both globally and locally.
Nonlinear tides are generated by hydrodynamic distortions of tides. A tidal wave is said to be nonlinear when its shape deviates from a pure sinusoidal wave. In mathematical terms, the wave owes its nonlinearity due to the nonlinear advection and frictional terms in the governing equations. These become more important in shallow-water regions such as in estuaries. Nonlinear tides are studied in the fields of coastal morphodynamics, coastal engineering and physical oceanography. The nonlinearity of tides has important implications for the transport of sediment.























































