Related Research Articles
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between those layers.
The Schumann resonances (SR) are a set of spectrum peaks in the extremely low frequency portion of the Earth's electromagnetic field spectrum. Schumann resonances are global electromagnetic resonances, generated and excited by lightning discharges in the cavity formed by the Earth's surface and the ionosphere.
Quantum turbulence is the name given to the turbulent flow – the chaotic motion of a fluid at high flow rates – of quantum fluids, such as superfluids. The idea that a form of turbulence might be possible in a superfluid via the quantized vortex lines was first suggested by Richard Feynman. The dynamics of quantum fluids are governed by quantum mechanics, rather than classical physics which govern classical (ordinary) fluids. Some examples of quantum fluids include superfluid helium, Bose–Einstein condensates (BECs), polariton condensates, and nuclear pasta theorized to exist inside neutron stars. Quantum fluids exist at temperatures below the critical temperature at which Bose-Einstein condensation takes place.
In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers and planar waveguides and to Bose–Einstein condensates confined to highly anisotropic, cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear media that have dispersion. Unlike the linear Schrödinger equation, the NLSE never describes the time evolution of a quantum state. The 1D NLSE is an example of an integrable model.
A direct numerical simulation (DNS) is a simulation in computational fluid dynamics (CFD) in which the Navier–Stokes equations are numerically solved without any turbulence model. This means that the whole range of spatial and temporal scales of the turbulence must be resolved. All the spatial scales of the turbulence must be resolved in the computational mesh, from the smallest dissipative scales, up to the integral scale , associated with the motions containing most of the kinetic energy. The Kolmogorov scale, , is given by
In fluid dynamics, a Tollmien–Schlichting wave is a streamwise unstable wave which arises in a bounded shear flow. It is one of the more common methods by which a laminar bounded shear flow transitions to turbulence. The waves are initiated when some disturbance interacts with leading edge roughness in a process known as receptivity. These waves are slowly amplified as they move downstream until they may eventually grow large enough that nonlinearities take over and the flow transitions to turbulence.
Vladimir Evgen'evich Zakharov was a Soviet and Russian mathematician and physicist. He was Regents' Professor of mathematics at The University of Arizona, director of the Mathematical Physics Sector at the Lebedev Physical Institute, and was on the committee of the Stefanos Pnevmatikos International Award. Zakharov's research interests covered physical aspects of nonlinear wave theory in plasmas, hydrodynamics, oceanology, geophysics, solid state physics, optics, and general relativity.
Liu Chen is an American theoretical physicist who has made original contributions to many aspects of plasma physics. He is known for the discoveries of kinetic Alfven waves, toroidal Alfven eigenmodes, and energetic particle modes; the theories of geomagnetic pulsations, Alfven wave heating, and fishbone oscillations, and the first formulation of nonlinear gyrokinetic equations. Chen retired from University of California, Irvine (UCI) in 2012, assuming the title professor emeritus of physics and astronomy.
In physics, nonlinear resonance is the occurrence of resonance in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequencies and modes – depends on the amplitude of the oscillations, while for linear systems this is independent of amplitude. The mixing of modes in non-linear systems is termed resonant interaction.
A nonlinear metamaterial is an artificially constructed material that can exhibit properties not yet found in nature. Its response to electromagnetic radiation can be characterized by its permittivity and material permeability. The product of the permittivity and permeability results in the refractive index. Unlike natural materials, nonlinear metamaterials can produce a negative refractive index. These can also produce a more pronounced nonlinear response than naturally occurring materials.
Magnetohydrodynamic turbulence concerns the chaotic regimes of magnetofluid flow at high Reynolds number. Magnetohydrodynamics (MHD) deals with what is a quasi-neutral fluid with very high conductivity. The fluid approximation implies that the focus is on macro length-and-time scales which are much larger than the collision length and collision time respectively.
Doubochinski's pendulum is a classical oscillator interacting with a high-frequency field in such a way that the oscillator takes on a discrete set of stable regimes of oscillation, each at a frequency near to the proper frequency of the oscillator, but each with a distinct, "quantized" amplitude. The phenomenon of amplitude quantization in this sort of coupled system was first discovered by the brothers Danil and Yakov Doubochinski in 1968–69.
Within statistics, the Kolmogorov–Zurbenko (KZ) filter was first proposed by A. N. Kolmogorov and formally defined by Zurbenko. It is a series of iterations of a moving average filter of length m, where m is a positive, odd integer. The KZ filter belongs to the class of low-pass filters. The KZ filter has two parameters, the length m of the moving average window and the number of iterations k of the moving average itself. It also can be considered as a special window function designed to eliminate spectral leakage.
Alan C. Newell is an Irish/American mathematician and Regents Professor at the University of Arizona. He was awarded a Guggenheim Fellowship in 1976 and in 2004 the John von Neumann Lecture for the Society for Industrial and Applied Mathematics. He was a Senior Scientist Humboldt Fellow in 1988–1989 and was elected a Fellow of the Society for Industrial and Applied Mathematics in 2009.
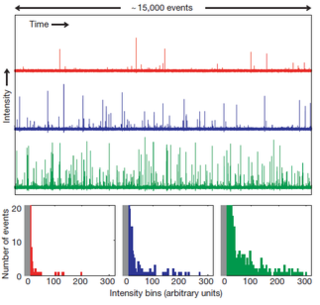
Optical rogue waves are rare pulses of light analogous to rogue or freak ocean waves. The term optical rogue waves was coined to describe rare pulses of broadband light arising during the process of supercontinuum generation—a noise-sensitive nonlinear process in which extremely broadband radiation is generated from a narrowband input waveform—in nonlinear optical fiber. In this context, optical rogue waves are characterized by an anomalous surplus in energy at particular wavelengths or an unexpected peak power. These anomalous events have been shown to follow heavy-tailed statistics, also known as L-shaped statistics, fat-tailed statistics, or extreme-value statistics. These probability distributions are characterized by long tails: large outliers occur rarely, yet much more frequently than expected from Gaussian statistics and intuition. Such distributions also describe the probabilities of freak ocean waves and various phenomena in both the man-made and natural worlds. Despite their infrequency, rare events wield significant influence in many systems. Aside from the statistical similarities, light waves traveling in optical fibers are known to obey the similar mathematics as water waves traveling in the open ocean, supporting the analogy between oceanic rogue waves and their optical counterparts. More generally, research has exposed a number of different analogies between extreme events in optics and hydrodynamic systems. A key practical difference is that most optical experiments can be done with a table-top apparatus, offer a high degree of experimental control, and allow data to be acquired extremely rapidly. Consequently, optical rogue waves are attractive for experimental and theoretical research and have become a highly studied phenomenon. The particulars of the analogy between extreme waves in optics and hydrodynamics may vary depending on the context, but the existence of rare events and extreme statistics in wave-related phenomena are common ground.
In continuum mechanics, an energy cascade involves the transfer of energy from large scales of motion to the small scales or a transfer of energy from the small scales to the large scales. This transfer of energy between different scales requires that the dynamics of the system is nonlinear. Strictly speaking, a cascade requires the energy transfer to be local in scale, evoking a cascading waterfall from pool to pool without long-range transfers across the scale domain.
Akira Hasegawa is a Japanese theoretical physicist and engineer who has worked in the U.S. and Japan. He is known for his work in the derivation of the Hasegawa–Mima equation, which describes fundamental plasma turbulence and the consequent generation of zonal flow that controls plasma diffusion. Hasegawa also made the discovery of optical solitons in glass fibers, a concept that is essential for high speed optical communications.
In nonlinear systems, a resonant interaction is the interaction of three or more waves, usually but not always of small amplitude. Resonant interactions occur when a simple set of criteria coupling wave-vectors and the dispersion equation are met. The simplicity of the criteria make technique popular in multiple fields. Its most prominent and well-developed forms appear in the study of gravity waves, but also finds numerous applications from astrophysics and biology to engineering and medicine. Theoretical work on partial differential equations provides insights into chaos theory; there are curious links to number theory. Resonant interactions allow waves to (elastically) scatter, diffuse or to become unstable. Diffusion processes are responsible for the eventual thermalization of most nonlinear systems; instabilities offer insight into high-dimensional chaos and turbulence.
Internal wave breaking is a process during which internal gravity waves attain a large amplitude compared to their length scale, become nonlinearly unstable and finally break. This process is accompanied by turbulent dissipation and mixing. As internal gravity waves carry energy and momentum from the environment of their inception, breaking and subsequent turbulent mixing affects the fluid characteristics in locations of breaking. Consequently, internal wave breaking influences even the large scale flows and composition in both the ocean and the atmosphere. In the atmosphere, momentum deposition by internal wave breaking plays a key role in atmospheric phenomena such as the Quasi-Biennial Oscillation and the Brewer-Dobson Circulation. In the deep ocean, mixing induced by internal wave breaking is an important driver of the meridional overturning circulation. On smaller scales, breaking-induced mixing is important for sediment transport and for nutrient supply to the photic zone. Most breaking of oceanic internal waves occurs in continental shelves, well below the ocean surface, which makes it a difficult phenomenon to observe.
Turbulent phenomena are observed universally in energetic fluid dynamics, associated with highly chaotic fluid motion involving excitations spread over a wide range of length scales. The particular features of turbulence are dependent on the fluid and geometry, and specifics of forcing and dissipation.
References
- Zakharov, V.E.; Lvov, V.S.; Falkovich, G.E. (1992). Kolmogorov Spectra of Turbulence I – Wave Turbulence. Berlin: Springer-Verlag. ISBN 3-540-54533-6.
- Nazarenko, Sergey (2011). Wave Turbulence. Springer-Verlag. ISBN 978-3642159411.
- Galtier, Sebastien (2023). Physics of Wave Turbulence. Cambridge University Press. ISBN 9781009275897.
- Kartashova, E. (2006). "A model of laminated turbulence". JETP Letters. 83 (7): 283–287. arXiv: physics/0512014 . Bibcode:2006JETPL..83..283K. doi:10.1134/S0021364006070058. S2CID 15630550.
- Kartashova, E. (2007). "Exact and quasi-resonances in discrete water wave turbulence". Physical Review Letters. 98 (21): 214502 (4 pp.). arXiv: math-ph/0701077 . Bibcode:2007PhRvL..98u4502K. doi:10.1103/PhysRevLett.98.214502. PMID 17677779. S2CID 12248807.
- Zakharov, V.E.; Korotkevich, A.O.; Pushkarev, A.N.; Dyachenko, A.I. (2005). "Mesoscopic wave turbulence". JETP Letters. 82 (8): 487–491. arXiv: physics/0508155 . Bibcode:2005physics...8155Z. doi:10.1134/1.2150867. S2CID 119002924.
- Kartashova, E. (2009). "Discrete wave turbulence". EPL. 87 (4): 44001 (5 pp.). arXiv: 0907.4406 . Bibcode:2009EL.....8744001K. doi:10.1209/0295-5075/87/44001. S2CID 18241042.
