Tidal resonance

Last updated
Tides at Portishead Dock in the Bristol Channel. An example of tidal resonance. PortisheadDocks Tides.JPG
Tides at Portishead Dock in the Bristol Channel. An example of tidal resonance.

In oceanography, a tidal resonance occurs when the tide excites one of the resonant modes of the ocean. [1] The effect is most striking when a continental shelf is about a quarter wavelength wide. Then an incident tidal wave can be reinforced by reflections between the coast and the shelf edge, the result producing a much higher tidal range at the coast.

Contents

Famous examples of this effect are found in the Bay of Fundy, where the world's highest tides are reportedly found, and in the Bristol Channel. Less well known is Leaf Bay, part of Ungava Bay near the entrance of Hudson Strait (Canada), which has tides similar to those of the Bay of Fundy. [2] Other resonant regions with large tides include the Patagonian Shelf and on the continental shelf of northwest Australia. [3]

Most of the resonant regions are also responsible for large fractions of the total amount of tidal energy dissipated in the oceans. Satellite altimeter data shows that the M2 tide dissipates approximately 2.5 TW, of which 261 GW is lost in the Hudson Bay complex, 208 GW on the European Shelves (including the Bristol Channel), 158 GW on the North-west Australian Shelf, 149 GW in the Yellow Sea and 112 GW on the Patagonian Shelf. [4]

Scale of the resonances

The speed of long waves in the ocean is given, to a good approximation, by , where g is the acceleration of gravity and h is the depth of the ocean. [5] [6] [7] For a typical continental shelf with a depth of 100 m, the speed is approximately 30 m/s. So if the tidal period is 12 hours, a quarter wavelength shelf will have a width of about 300 km.

With a narrower shelf, there is still a resonance but it is mismatched to the frequency of the tides and so has less effect on tidal amplitudes. However the effect is still enough to partly explain why tides along a coast lying behind a continental shelf are often higher than at offshore islands in the deep ocean (one of the additional partial explanations being Green's law). Resonances also generate strong tidal currents and it is the turbulence caused by the currents which is responsible for the large amount of tidal energy dissipated in such regions.

In the deep ocean, where the depth is typically 4000 m, the speed of long waves increases to approximately 200 m/s. The difference in speed, when compared to the shelf, is responsible for reflections at the continental shelf edge. Away from resonance this can reduce tidal energy moving onto the shelf. However near a resonant frequency the phase relationship, between the waves on the shelf and in the deep ocean, can have the effect of drawing energy onto the shelf.

The increased speed of long waves in the deep ocean means that the tidal wavelength there is of order 10,000 km. As the ocean basins have a similar size, they also have the potential of being resonant. [8] [9] In practice deep ocean resonances are difficult to observe, probably because the deep ocean loses tidal energy too rapidly to the resonant shelves.

See also

Related Research Articles

Tide Rise and fall of the sea level under astronomical gravitational influences

Tides are the rise and fall of sea levels caused by the combined effects of the gravitational forces exerted by the Moon and the Sun, and the rotation of the Earth.

Tsunami Series of water waves caused by the displacement of a large volume of a body of water

A tsunami is a series of waves in a water body caused by the displacement of a large volume of water, generally in an ocean or a large lake. Earthquakes, volcanic eruptions and other underwater explosions above or below water all have the potential to generate a tsunami. Unlike normal ocean waves, which are generated by wind, or tides, which are generated by the gravitational pull of the Moon and the Sun, a tsunami is generated by the displacement of water.

Tidal power Technology to convert the energy from tides into useful forms of power

Tidal power or tidal energy is harnessed by converting energy from tides into useful forms of power, mainly electricity using various methods.

Amphidromic point point of zero amplitude of one harmonic constituent of the tide

An amphidromic point, also called a tidal node, is a geographical location which has zero tidal amplitude for one harmonic constituent of the tide. The tidal range for that harmonic constituent increases with distance from this point.

Physical oceanography The study of physical conditions and physical processes within the ocean

Physical oceanography is the study of physical conditions and physical processes within the ocean, especially the motions and physical properties of ocean waters.

Seiche Standing wave in an enclosed or partially enclosed body of water

A seiche is a standing wave in an enclosed or partially enclosed body of water. Seiches and seiche-related phenomena have been observed on lakes, reservoirs, swimming pools, bays, harbours and seas. The key requirement for formation of a seiche is that the body of water be at least partially bounded, allowing the formation of the standing wave.

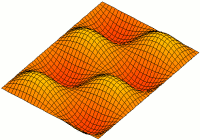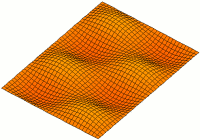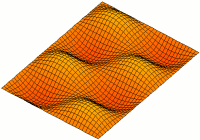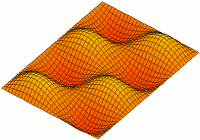
Resonator Device or system that exhibits resonance

A resonator is a device or system that exhibits resonance or resonant behavior. That is, it naturally oscillates with greater amplitude at some frequencies, called resonant frequencies, than at other frequencies. The oscillations in a resonator can be either electromagnetic or mechanical. Resonators are used to either generate waves of specific frequencies or to select specific frequencies from a signal. Musical instruments use acoustic resonators that produce sound waves of specific tones. Another example is quartz crystals used in electronic devices such as radio transmitters and quartz watches to produce oscillations of very precise frequency.

Wind wave Surface waves generated by wind on open water

In fluid dynamics, wind waves, or wind-generated waves, are water surface waves that occur on the free surface of bodies of water. They result from the wind blowing over a fluid surface, where the contact distance in the direction of the wind is known as the fetch. Waves in the oceans can travel thousands of miles before reaching land. Wind waves on Earth range in size from small ripples, to waves over 100 ft (30 m) high, being limited by wind speed, duration, fetch, and water depth.

Internal wave Gravity waves that oscillate within a fluid medium with density variation with depth, rather than on the surface

Internal waves are gravity waves that oscillate within a fluid medium, rather than on its surface. To exist, the fluid must be stratified: the density must change with depth/height due to changes, for example, in temperature and/or salinity. If the density changes over a small vertical distance, the waves propagate horizontally like surface waves, but do so at slower speeds as determined by the density difference of the fluid below and above the interface. If the density changes continuously, the waves can propagate vertically as well as horizontally through the fluid.

Walter Munk American oceanographer

Walter Heinrich Munk was an American physical oceanographer. One of the first scientists to bring statistical methods to the analysis of oceanographic data, Munk is noted for creating fruitful areas of research that continue to be explored by other scientists. Munk's work garnered him many prestigious awards including the National Medal of Science, the Kyoto Prize, and induction to the French Legion of Honour.

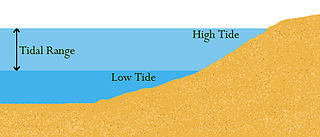
Tidal range Vertical difference between the high tide and the succeeding low tide

Tidal range is the height difference between high tide and low tide. Tides are the rise and fall of sea levels caused by gravitational forces exerted by the Moon and Sun and the rotation of Earth. Tidal range is not constant but changes depending on the locations of the Moon and Sun.

Atmospheric tides are global-scale periodic oscillations of the atmosphere. In many ways they are analogous to ocean tides. Atmospheric tides can be excited by:

The following outline is provided as an overview of and introduction to Oceanography.

Wave shoaling The effect by which surface waves entering shallower water change in wave height

In fluid dynamics, wave shoaling is the effect by which surface waves entering shallower water change in wave height. It is caused by the fact that the group velocity, which is also the wave-energy transport velocity, changes with water depth. Under stationary conditions, a decrease in transport speed must be compensated by an increase in energy density in order to maintain a constant energy flux. Shoaling waves will also exhibit a reduction in wavelength while the frequency remains constant.

Ocean power in New Zealand

New Zealand has large ocean energy resources but does not yet generate any power from them. TVNZ reported in 2007 that over 20 wave and tidal power projects are currently under development. However, not a lot of public information is available about these projects. The Aotearoa Wave and Tidal Energy Association was established in 2006 to "promote the uptake of marine energy in New Zealand". According to their 10 February 2008 newsletter, they have 59 members. However, the association doesn't list its members.

Internal tides are generated as the surface tides move stratified water up and down sloping topography, which produces a wave in the ocean interior. So internal tides are internal waves at a tidal frequency. The other major source of internal waves is the wind which produces internal waves near the inertial frequency. When a small water parcel is displaced from its equilibrium position, it will return either downwards due to gravity or upwards due to buoyancy. The water parcel will overshoot its original equilibrium position and this disturbance will set off an internal gravity wave. Munk (1981) notes, "Gravity waves in the ocean's interior are as common as waves at the sea surface-perhaps even more so, for no one has ever reported an interior calm."

Infragravity wave Surface gravity waves with frequencies lower than the wind waves

Infragravity waves are surface gravity waves with frequencies lower than the wind waves – consisting of both wind sea and swell – thus corresponding with the part of the wave spectrum lower than the frequencies directly generated by forcing through the wind.

Marine habitats A habitat that supports marine life

Marine habitats are habitats that support marine life. Marine life depends in some way on the saltwater that is in the sea. A habitat is an ecological or environmental area inhabited by one or more living species. The marine environment supports many kinds of these habitats.

Long-period tides Gravitational tides, typically with amplitudes of a few centimeters or less and periods longer than one day, generated by changes in the Earths orientation relative to the Sun, Moon, and Jupiter

Long-period tides are gravitational tides with periods longer than one day, typically with amplitudes of a few centimeters or less. Long-period tidal constituents with relatively strong forcing include the lunar fortnightly (Mf) and lunar monthly (Ms) as well as the solar semiannual (Ssa) and solar annual (Sa) constituents.

In nonlinear systems, a resonant interaction is the interaction of three or more waves, usually but not always of small amplitude. Resonant interactions occur when a simple set of criteria coupling wave-vectors and the dispersion equation are met. The simplicty of the criteria make technique popular in multiple fields. Its most prominent and well-developed forms appear in the study of gravity waves, but also finds numerous applications from astrophysics and biology to engineering and medicine. Theoretical work on partial differential equations provides insights into chaos theory; there are curious links to number theory. Resonant interactions allow waves to (elastically) scatter, diffuse or to become unstable. Diffusion processes are responsible for the eventual thermalization of most nonlinear systems; instabilities offer insight into high-dimensional chaos and turbulence.

References

  1. ↑ Platzman, G.W. (1991), "Tidal Evidence for Ocean Normal Modes", in Parker, B.P. (ed.), Tidal Hydrodynamics, New York: John Wiley & Sons, p. 883
  2. ↑ O'Reilly, C.T.; Solvason, R.; Solomon, C. (2005). J. Ryan (ed.). "Where are the World's Largest Tides". BIO Annual Report: 2004 in Review. Biotechnol. Ind. Org., Washington, D. C.: 44–46.
  3. ↑ Webb, D.J. (1976). "A Model of Continental-shelf Resonances". Deep-Sea Research. 23 (1): 1–15. Bibcode:1976DSROA..23....1W. doi:10.1016/0011-7471(76)90804-4.
  4. ↑ Egbert, G.D.; Ray, R. (2001). "Estimates of M2 tidal dissipation from TOPEX/Poseidon altimeter data". Journal of Geophysical Research. 106 (C10): 22475–22502. Bibcode:2001JGR...10622475E. doi:10.1029/2000JC000699.
  5. ↑ Segar, D.A. (2007). Introduction to Ocean Science. New York: W.W. Norton. pp. 581+.
  6. ↑ Knauss, J.A. (1997). Introduction to Physical Oceanography. Long Grove, USA: Waveland Press. p. 309.
  7. ↑ Defant, A. (1961). Introduction to Physical Oceanography. II. Oxford: Pergamon Press. p. 598.
  8. ↑ Platzman, G.W.; Curtis, G.A.; Hansen, K.S.; Slater, R.D. (1981). "Normal Modes of the World ocean. Part II: Description of Modes in the Period Range 8 to 80 Hours". Journal of Physical Oceanography . 11 (5): 579–603. Bibcode:1981JPO....11..579P. doi: 10.1175/1520-0485(1981)011<0579:NMOTWO>2.0.CO;2 .
  9. ↑ Webb, D.J. (1973). "Tidal Resonance in the Coral Sea". Nature . 243 (5409): 511. Bibcode:1973Natur.243..511W. doi: 10.1038/243511a0 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.