In optimization, a gradient method is an algorithm to solve problems of the form
with the search directions defined by the gradient of the function at the current point. Examples of gradient methods are the gradient descent and the conjugate gradient.
Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
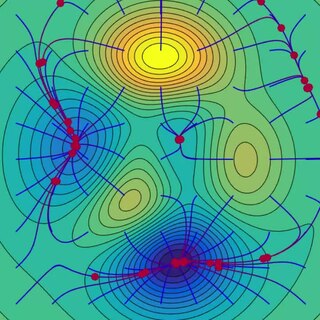
Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum of that function; the procedure is then known as gradient ascent.
In numerical analysis, hill climbing is a mathematical optimization technique which belongs to the family of local search. It is an iterative algorithm that starts with an arbitrary solution to a problem, then attempts to find a better solution by making an incremental change to the solution. If the change produces a better solution, another incremental change is made to the new solution, and so on until no further improvements can be found.
The Gauss–Newton algorithm is used to solve non-linear least squares problems. It is a modification of Newton's method for finding a minimum of a function. Unlike Newton's method, the Gauss–Newton algorithm can only be used to minimize a sum of squared function values, but it has the advantage that second derivatives, which can be challenging to compute, are not required.
Stochastic gradient descent is an iterative method for optimizing an objective function with suitable smoothness properties. It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient by an estimate thereof. Especially in high-dimensional optimization problems this reduces the computational burden, achieving faster iterations in trade for a lower convergence rate.
In calculus, Newton's method is an iterative method for finding the roots of a differentiable function F, which are solutions to the equation F (x) = 0. As such, Newton's method can be applied to the derivative f ′ of a twice-differentiable function f to find the roots of the derivative, also known as the critical points of f. These solutions may be minima, maxima, or saddle points; see section "Several variables" in Critical point (mathematics) and also section "Geometric interpretation" in this article. This is relevant in optimization, which aims to find (global) minima of the function f.
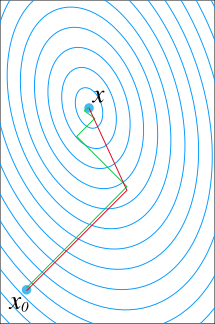
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems.
In optimization, the line search strategy is one of two basic iterative approaches to find a local minimum of an objective function . The other approach is trust region.
In the unconstrained minimization problem, the Wolfe conditions are a set of inequalities for performing inexact line search, especially in quasi-Newton methods, first published by Philip Wolfe in 1969.
In mathematics, preconditioning is the application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solving methods. Preconditioning is typically related to reducing a condition number of the problem. The preconditioned problem is then usually solved by an iterative method.
In numerical optimization, the nonlinear conjugate gradient method generalizes the conjugate gradient method to nonlinear optimization. For a quadratic function
Gradient boosting is a machine learning technique for regression, classification and other tasks, which produces a prediction model in the form of an ensemble of weak prediction models, typically decision trees. When a decision tree is the weak learner, the resulting algorithm is called gradient boosted trees, which usually outperforms random forest. It builds the model in a stage-wise fashion like other boosting methods do, and it generalizes them by allowing optimization of an arbitrary differentiable loss function.
Coordinate descent is an optimization algorithm that successively minimizes along coordinate directions to find the minimum of a function. At each iteration, the algorithm determines a coordinate or coordinate block via a coordinate selection rule, then exactly or inexactly minimizes over the corresponding coordinate hyperplane while fixing all other coordinates or coordinate blocks. A line search along the coordinate direction can be performed at the current iterate to determine the appropriate step size. Coordinate descent is applicable in both differentiable and derivative-free contexts.
Randomized (Block) Coordinate Descent Method is an optimization algorithm popularized by Nesterov (2010) and Richtárik and Takáč (2011). The first analysis of this method, when applied to the problem of minimizing a smooth convex function, was performed by Nesterov (2010). In Nesterov's analysis the method needs to be applied to a quadratic perturbation of the original function with an unknown scaling factor. Richtárik and Takáč (2011) give iteration complexity bounds which do not require this, i.e., the method is applied to the objective function directly. Furthermore, they generalize the setting to the problem of minimizing a composite function, i.e., sum of a smooth convex and a convex block-separable function:
Adaptive coordinate descent is an improvement of the coordinate descent algorithm to non-separable optimization by the use of adaptive encoding. The adaptive coordinate descent approach gradually builds a transformation of the coordinate system such that the new coordinates are as decorrelated as possible with respect to the objective function. The adaptive coordinate descent was shown to be competitive to the state-of-the-art evolutionary algorithms and has the following invariance properties:
Proximal gradient methods are a generalized form of projection used to solve non-differentiable convex optimization problems.
Proximal gradientmethods for learning is an area of research in optimization and statistical learning theory which studies algorithms for a general class of convex regularization problems where the regularization penalty may not be differentiable. One such example is regularization of the form
Derivative-free optimization is a discipline in mathematical optimization that does not use derivative information in the classical sense to find optimal solutions: Sometimes information about the derivative of the objective function f is unavailable, unreliable or impractical to obtain. For example, f might be non-smooth, or time-consuming to evaluate, or in some way noisy, so that methods that rely on derivatives or approximate them via finite differences are of little use. The problem to find optimal points in such situations is referred to as derivative-free optimization, algorithms that do not use derivatives or finite differences are called derivative-free algorithms.
In mathematical optimization, the problem of non-negative least squares (NNLS) is a type of constrained least squares problem where the coefficients are not allowed to become negative. That is, given a matrix A and a (column) vector of response variables y, the goal is to find
|  | |||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
