Related Research Articles
Quadratic programming (QP) is the process of solving certain mathematical optimization problems involving quadratic functions. Specifically, one seeks to optimize a multivariate quadratic function subject to linear constraints on the variables. Quadratic programming is a type of nonlinear programming.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
Multi-disciplinary design optimization (MDO) is a field of engineering that uses optimization methods to solve design problems incorporating a number of disciplines. It is also known as multidisciplinary system design optimization (MSDO), and multidisciplinary design analysis and optimization (MDAO).
In mathematics, nonlinear programming (NLP) is the process of solving an optimization problem where some of the constraints are not linear equalities or the objective function is not a linear function. An optimization problem is one of calculation of the extrema of an objective function over a set of unknown real variables and conditional to the satisfaction of a system of equalities and inequalities, collectively termed constraints. It is the sub-field of mathematical optimization that deals with problems that are not linear.
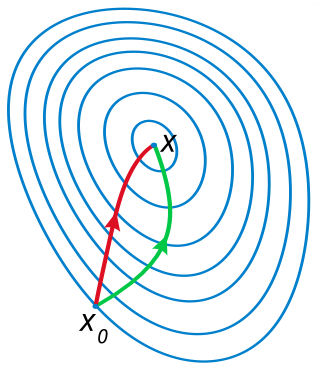
In calculus, Newton's method is an iterative method for finding the roots of a differentiable function , which are solutions to the equation . As such, Newton's method can be applied to the derivative of a twice-differentiable function to find the roots of the derivative, also known as the critical points of . These solutions may be minima, maxima, or saddle points; see section "Several variables" in Critical point (mathematics) and also section "Geometric interpretation" in this article. This is relevant in optimization, which aims to find (global) minima of the function .
In optimization, line search is a basic iterative approach to find a local minimum of an objective function . It first finds a descent direction along which the objective function will be reduced, and then computes a step size that determines how far should move along that direction. The descent direction can be computed by various methods, such as gradient descent or quasi-Newton method. The step size can be determined either exactly or inexactly.
In mathematical optimization, the active-set method is an algorithm used to identify the active constraints in a set of inequality constraints. The active constraints are then expressed as equality constraints, thereby transforming an inequality-constrained problem into a simpler equality-constrained subproblem.
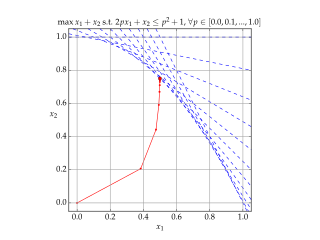
Interior-point methods are algorithms for solving linear and non-linear convex optimization problems. IPMs combine two advantages of previously-known algorithms:
The Frank–Wolfe algorithm is an iterative first-order optimization algorithm for constrained convex optimization. Also known as the conditional gradient method, reduced gradient algorithm and the convex combination algorithm, the method was originally proposed by Marguerite Frank and Philip Wolfe in 1956. In each iteration, the Frank–Wolfe algorithm considers a linear approximation of the objective function, and moves towards a minimizer of this linear function.
Sequential quadratic programming (SQP) is an iterative method for constrained nonlinear optimization which may be considered a quasi-Newton method. SQP methods are used on mathematical problems for which the objective function and the constraints are twice continuously differentiable, but not necessarily convex.
Penalty methods are a certain class of algorithms for solving constrained optimization problems.
Naum Zuselevich Shor was a Soviet and Ukrainian mathematician specializing in optimization.
Sequential minimal optimization (SMO) is an algorithm for solving the quadratic programming (QP) problem that arises during the training of support-vector machines (SVM). It was invented by John Platt in 1998 at Microsoft Research. SMO is widely used for training support vector machines and is implemented by the popular LIBSVM tool. The publication of the SMO algorithm in 1998 has generated a lot of excitement in the SVM community, as previously available methods for SVM training were much more complex and required expensive third-party QP solvers.
Robert J. Vanderbei is an American mathematician and Emeritus Professor in the Department of Operations Research and Financial Engineering at Princeton University.
Augmented Lagrangian methods are a certain class of algorithms for solving constrained optimization problems. They have similarities to penalty methods in that they replace a constrained optimization problem by a series of unconstrained problems and add a penalty term to the objective, but the augmented Lagrangian method adds yet another term designed to mimic a Lagrange multiplier. The augmented Lagrangian is related to, but not identical with, the method of Lagrange multipliers.
The FICO Xpress optimizer is a commercial optimization solver for linear programming (LP), mixed integer linear programming (MILP), convex quadratic programming (QP), convex quadratically constrained quadratic programming (QCQP), second-order cone programming (SOCP) and their mixed integer counterparts. Xpress includes a general purpose non-linear solver, Xpress NonLinear, including a successive linear programming algorithm, and Artelys Knitro.
MINOS is a Fortran software package for solving linear and nonlinear mathematical optimization problems. MINOS may be used for linear programming, quadratic programming, and more general objective functions and constraints, and for finding a feasible point for a set of linear or nonlinear equalities and inequalities.
Artelys Knitro is a commercial software package for solving large scale nonlinear mathematical optimization problems.
Sequential linear-quadratic programming (SLQP) is an iterative method for nonlinear optimization problems where objective function and constraints are twice continuously differentiable. Similarly to sequential quadratic programming (SQP), SLQP proceeds by solving a sequence of optimization subproblems. The difference between the two approaches is that:
References
- ↑ ( Nocedal & Wright 2006 , p. 551)
- ↑ ( Bazaraa, Sherali & Shetty 1993 , p. 432)
- ↑ ( Palacios-Gomez, Lasdon & Enquist 1982 )
