
In computer science, an AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if

In mathematics, the logarithm to baseb is the inverse function of exponentiation with base b. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. For example, since 1000 = 103, the logarithm base of 1000 is 3, or log10 (1000) = 3. The logarithm of x to base b is denoted as logb (x), or without parentheses, logb x. When the base is clear from the context or is irrelevant it is sometimes written log x.
In mathematics, the mean value theorem states, roughly, that for a given planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints. It is one of the most important results in real analysis. This theorem is used to prove statements about a function on an interval starting from local hypotheses about derivatives at points of the interval.

In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is The parameter is the mean or expectation of the distribution, while the parameter is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate.
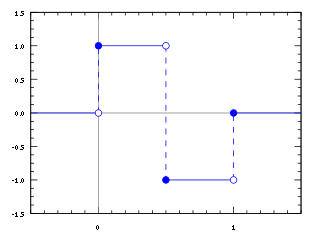
In mathematics, the Haar wavelet is a sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal basis. The Haar sequence is now recognised as the first known wavelet basis and is extensively used as a teaching example.
The calculus of variations is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations.
In calculus, integration by substitution, also known as u-substitution, reverse chain rule or change of variables, is a method for evaluating integrals and antiderivatives. It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule "backwards."

In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the function f(x) that maps x to 1/x, is one of the simplest examples of a function which is its own inverse (an involution).

In number theory, the Mertens function is defined for all positive integers n as
Branch and bound is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution. It is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm.
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of , its subsequence has a low discrepancy.

In numerical analysis, the secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function f. The secant method can be thought of as a finite-difference approximation of Newton's method, so it is considered a quasi-Newton method. Historically, it is as an evolution of the method of false position, which predates Newton's method by over 3000 years.

In mathematics, the bisection method is a root-finding method that applies to any continuous function for which one knows two values with opposite signs. The method consists of repeatedly bisecting the interval defined by these values and then selecting the subinterval in which the function changes sign, and therefore must contain a root. It is a very simple and robust method, but it is also relatively slow. Because of this, it is often used to obtain a rough approximation to a solution which is then used as a starting point for more rapidly converging methods. The method is also called the interval halving method, the binary search method, or the dichotomy method.
In mathematics, the regula falsi, method of false position, or false position method is a very old method for solving an equation with one unknown; this method, in modified form, is still in use. In simple terms, the method is the trial and error technique of using test ("false") values for the variable and then adjusting the test value according to the outcome. This is sometimes also referred to as "guess and check". Versions of the method predate the advent of algebra and the use of equations.
The TPK algorithm is a simple program introduced by Donald Knuth and Luis Trabb Pardo to illustrate the evolution of computer programming languages. In their 1977 work "The Early Development of Programming Languages", Trabb Pardo and Knuth introduced a small program that involved arrays, indexing, mathematical functions, subroutines, I/O, conditionals and iteration. They then wrote implementations of the algorithm in several early programming languages to show how such concepts were expressed.

The Gauss–Newton algorithm is used to solve non-linear least squares problems, which is equivalent to minimizing a sum of squared function values. It is an extension of Newton's method for finding a minimum of a non-linear function. Since a sum of squares must be nonnegative, the algorithm can be viewed as using Newton's method to iteratively approximate zeroes of the components of the sum, and thus minimizing the sum. In this sense, the algorithm is also an effective method for solving overdetermined systems of equations. It has the advantage that second derivatives, which can be challenging to compute, are not required.
In optimization, line search is a basic iterative approach to find a local minimum of an objective function . It first finds a descent direction along which the objective function will be reduced, and then computes a step size that determines how far should move along that direction. The descent direction can be computed by various methods, such as gradient descent or quasi-Newton method. The step size can be determined either exactly or inexactly.

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z).
In mathematics, the ATS theorem is the theorem on the approximation of a trigonometric sum by a shorter one. The application of the ATS theorem in certain problems of mathematical and theoretical physics can be very helpful.




























![Diagram of the golden section search for a minimum. The initial interval enclosed by X1 and X4 is divided into three intervals, and f[X] is evaluated at each of the four Xi. The two intervals containing the minimum of f(Xi) are then selected, and a third interval and functional value are calculated, and the process is repeated until termination conditions are met. The three interval widths are always in the ratio c:cr:c where r = ph - 1 = 0.618... and c = 1 - r = 0.382..., ph being the golden ratio. This choice of interval ratios is the only one that allows the ratios to be maintained during an iteration. Diagram of a golden section search.jpg](http://upload.wikimedia.org/wikipedia/commons/thumb/6/68/Diagram_of_a_golden_section_search.jpg/325px-Diagram_of_a_golden_section_search.jpg)













