List of disproved mathematical ideas

Last updated July 03, 2023

In mathematics, ideas are supposedly not accepted as fact until they have been rigorously proved. However, there have been some ideas that were fairly accepted in the past but which were subsequently shown to be false. This article is meant to serve as a repository for compiling a list of such ideas.

The idea of the Pythagoreans that all numbers can be expressed as a ratio of two whole numbers. This was disproved by one of Pythagoras' own disciples, Hippasus, who showed that the square root of two is what we today call an irrational number. One story claims that he was thrown off the ship in which he and some other Pythagoreans were sailing because his discovery was too heretical.^[1]
Fermat conjectured that all numbers of the form $2^{2^{m}}+1$ (known as Fermat numbers) were prime. However, this conjecture was disproved by Euler.^[2]
The idea that transcendental numbers were unusual. Disproved by Georg Cantor who showed that there are so many transcendental numbers that it is impossible to make a one-to-one mapping between them and the algebraic numbers. In other words, the cardinality of the set of transcendentals (denoted $\beth _{1}$ ) is greater than that of the set of algebraic numbers ( $\aleph _{0}$ ).^[3]
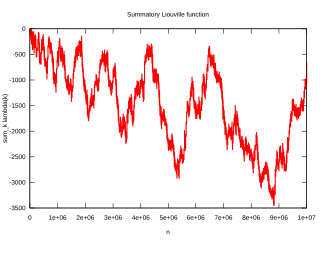
Bernhard Riemann, at the end of his famous 1859 paper "On the Number of Primes Less Than a Given Magnitude", stated (based on his results) that the logarithmic integral gives a somewhat too high estimate of the prime-counting function. The evidence also seemed to indicate this. However, in 1914 J. E. Littlewood proved that this was not always the case, and in fact it is now known that the first x for which $\pi (x)>\mathrm {li} (x)$ occurs somewhere before 10³¹⁷. See Skewes' number for more detail.
Naïvely it might be expected that a continuous function must have a derivative or else that the set of points where it is not differentiable should be "small" in some sense. This was disproved in 1872 by Karl Weierstrass, using earlier found examples of functions that were continuous but nowhere differentiable (see Weierstrass function). According to Weierstrass in his paper, earlier mathematicians including Gauss had often assumed that such functions did not exist.
It was conjectured in 1919 by George Pólya, based on the evidence, that most numbers less than any particular limit have an odd number of prime factors. However, this Pólya conjecture was disproved in 1958. It turns out that for some values of the limit (such as values a bit more than 906 million),^[4]^[5] most numbers less than the limit have an even number of prime factors.
Erik Christopher Zeeman tried for 7 years to prove that one cannot untie a knot on a 4-sphere. Then one day he decided to try to prove the opposite, and he succeeded in a few hours.^[6]
A "theorem" of Jan-Erik Roos in 1961 stated that in an [AB4^*] abelian category, lim¹ vanishes on Mittag-Leffler sequences. This "theorem" was used by many people since then, but it was disproved by counterexample in 2002 by Amnon Neeman.^[7]
Euler's sum of powers conjecture

Related Research Articles

<span class="mw-page-title-main">Conjecture</span> Proposition in mathematics that is unproven

In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's Last Theorem, have shaped much of mathematical history as new areas of mathematics are developed in order to prove them.

Euler's conjecture is a disproved conjecture in mathematics related to Fermat's Last Theorem. It was proposed by Leonhard Euler in 1769. It states that for all integers $n$ and $k$ greater than 1, if the sum of $n$ many $k$ th powers of positive integers is itself a $k$ th power, then $n$ is greater than or equal to $k$ :

Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics." Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers, or defined as generalizations of the integers.

<span class="mw-page-title-main">Prime number</span> Evenly divided only by 1 or itself

A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.

In mathematics, a transcendental number is a real or complex number that is not algebraic – that is, not the root of a non-zero polynomial of finite degree with rational coefficients. The best known transcendental numbers are $π$ and $e$ .

A counterexample is any exception to a generalization. In logic a counterexample disproves the generalization, and does so rigorously in the fields of mathematics and philosophy. For example, the fact that "student John Smith is not lazy" is a counterexample to the generalization “students are lazy”, and both a counterexample to, and disproof of, the universal quantification “all students are lazy.”

Transcendental number theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.

In mathematics, specifically transcendental number theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.

The Beal conjecture is the following conjecture in number theory:

In mathematics, a proof of impossibility is a proof that demonstrates that a particular problem cannot be solved as described in the claim, or that a particular set of problems cannot be solved in general. Such a case is also known as a negative proof, proof of an impossibility theorem, or negative result. Proofs of impossibility often are the resolutions to decades or centuries of work attempting to find a solution, eventually proving that there is no solution. Proving that something is impossible is usually much harder than the opposite task, as it is often necessary to develop a proof that works in general, rather than to just show a particular example. Impossibility theorems are usually expressible as negative existential propositions or universal propositions in logic.

<span class="mw-page-title-main">Pólya conjecture</span> Disproved conjecture in number theory

In number theory, the Pólya conjecture stated that "most" of the natural numbers less than any given number have an odd number of prime factors. The conjecture was set forth by the Hungarian mathematician George Pólya in 1919, and proved false in 1958 by C. Brian Haselgrove. Though mathematicians typically refer to this statement as the Pólya conjecture, Pólya never actually conjectured that the statement was true; rather, he showed that the truth of the statement would imply the Riemann hypothesis. For this reason, it is more accurately called "Pólya's problem".

The Swiss mathematician Leonhard Euler (1707–1783) is among the most prolific and successful mathematicians in the history of the field. His seminal work had a profound impact in numerous areas of mathematics and he is widely credited for introducing and popularizing modern notation and terminology.

<span class="mw-page-title-main">Fermat's Last Theorem</span> 17th-century conjecture proved by Andrew Wiles in 1994

In number theory, Fermat's Last Theorem states that no three positive integers $a$ , $b$ , and $c$ satisfy the equation $a n + b n = c n$ for any integer value of $n$ greater than 2. The cases $n = 1$ and $n = 2$ have been known since antiquity to have infinitely many solutions.

This is a timeline of pure and applied mathematics history. It is divided here into three stages, corresponding to stages in the development of mathematical notation: a "rhetorical" stage in which calculations are described purely by words, a "syncopated" stage in which quantities and common algebraic operations are beginning to be represented by symbolic abbreviations, and finally a "symbolic" stage, in which comprehensive notational systems for formulas are the norm.

In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being incommensurable, meaning that they share no "measure" in common, that is, there is no length, no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself.

Wiles's proof of Fermat's Last Theorem is a proof by British mathematician Andrew Wiles of a special case of the modularity theorem for elliptic curves. Together with Ribet's theorem, it provides a proof for Fermat's Last Theorem. Both Fermat's Last Theorem and the modularity theorem were almost universally considered inaccessible to prove by contemporaneous mathematicians, meaning that they were believed to be impossible to prove using current knowledge.

The Lander, Parkin, and Selfridge conjecture concerns the integer solutions of equations which contain sums of like powers. The equations are generalisations of those considered in Fermat's Last Theorem. The conjecture is that if the sum of some k-th powers equals the sum of some other k-th powers, then the total number of terms in both sums combined must be at least k.

References

↑ Farlow, Stanley J. (2014). Paradoxes in Mathematics. Courier Corporation. p. 57. ISBN 978-0-486-49716-7.
↑ Krizek, Michal; Luca, Florian; Somer, Lawrence (2001). 17 Lectures on Fermat Numbers: From Number Theory to Geometry. Springer. p. 1. doi:10.1007/978-0-387-21850-2. ISBN 0-387-95332-9.
↑ McQuarrie, Donald Allan (2003). Mathematical Methods for Scientists and Engineers. University Science Books. p. 711.
↑ Lehman, R. S. (1960). "On Liouville's function". Mathematics of Computation . 14 (72): 311–320. doi: 10.1090/S0025-5718-1960-0120198-5 . JSTOR 2003890. MR 0120198.
↑ Tanaka, M. (1980). "A Numerical Investigation on Cumulative Sum of the Liouville Function". Tokyo Journal of Mathematics . 3 (1): 187–189. doi: 10.3836/tjm/1270216093 . MR 0584557.
↑ Why mathematics is beautiful in New Scientist, 21 July 2007, p. 48
↑ Neeman, Amnon (2002). "A counterexample to a 1961 "theorem" in homological algebra". Inventiones mathematicae. 148: 397–420. doi:10.1007/s002220100197.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Farlow, Stanley J. (2014). Paradoxes in Mathematics. Courier Corporation. p. 57. ISBN 978-0-486-49716-7.

[2] Krizek, Michal; Luca, Florian; Somer, Lawrence (2001). 17 Lectures on Fermat Numbers: From Number Theory to Geometry. Springer. p. 1. doi:10.1007/978-0-387-21850-2. ISBN 0-387-95332-9.

[3] McQuarrie, Donald Allan (2003). Mathematical Methods for Scientists and Engineers. University Science Books. p. 711.

[4] Lehman, R. S. (1960). "On Liouville's function". Mathematics of Computation . 14 (72): 311–320. doi: 10.1090/S0025-5718-1960-0120198-5 . JSTOR 2003890. MR 0120198.

[5] Tanaka, M. (1980). "A Numerical Investigation on Cumulative Sum of the Liouville Function". Tokyo Journal of Mathematics . 3 (1): 187–189. doi: 10.3836/tjm/1270216093 . MR 0584557.

[6] Why mathematics is beautiful in New Scientist, 21 July 2007, p. 48

[7] Neeman, Amnon (2002). "A counterexample to a 1961 "theorem" in homological algebra". Inventiones mathematicae. 148: 397–420. doi:10.1007/s002220100197.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

List of disproved mathematical ideas

See also

Related Research Articles

References