Macroharmony

Last updated

In music analysis, the macroharmony is what comprises the discrete pitch classes within a given (structural) duration of time. [1]

Contents

Definitions

There are slightly different definitions of macroharmony in the literature. In general, it may be said to determine pitch content within some duration of a musical composition. [2] Dmitri Tymoczko defined it as "the total collection of notes used over small stretches of time". [3] Neil Newton defined it as "the collection of pitches from which harmonies are sourced". [4] Ciro Scotto wrote that it is "a large harmony that subsumes the individual chords", adding that he used it more specifically to denote pitch-class subsets. [5] Julian Hook related it to the concept of a field of pitch classes, noting that the difference was one of terminology. [2]

Tymoczko's Geometry

Scotto suggested the term to Tymoczko, who introduced and defined it in A Geometry of Music (2011). [6] Tymoczko sought to discuss "music that is neither classically tonal nor completely atonal" (see chromaticism and nonchord tones). [7] He observed that a macroharmony of between five and eight pitch classes, or a limited macroharmony, typically contributed to a sense of tonality. [8] He included this feature, limited macroharmony, as one among five general (universal) features of "virtually all" music. The others were conjunct melodic motion, acoustic consonance, harmonic consistency, and pitch centricity. He considered their (non-)interaction, relative importance, and mutual reinforcement. [9]

Of macroharmonies specifically, he asked: [10]

He proposed to show the rate at which pitch classes are used with "pitch-class circulation graphs" and the number and relative proportion of pitch classes on a large scale with "global macroharmonic profiles". [10]

Relation to scale

In general, macroharmony may be understood in some relation to musical scales. [11] Theoretically, the pitch-class content of tonal music may be that of the chromatic scale. [11] Practically, it is often limited to that of modes, especially the major or minor diatonic scales as subsets of the chromatic scale. [11] [b] In a similar way, though scales may in fact constitute the entire pitch-class content of a given tuning system or the macroharmony of some portion of a composition, they are nonetheless defined as subsets of the macroharmony within the context of Tymoczko's project. [12]

See also

Related Research Articles

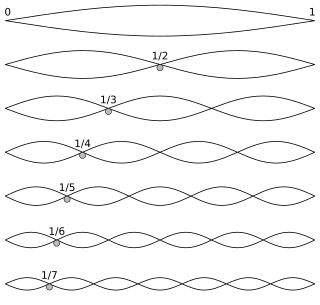
<span class="mw-page-title-main">Harmonic series (music)</span> Sequence of frequencies

The harmonic series is the sequence of harmonics, musical tones, or pure tones whose frequency is an integer multiple of a fundamental frequency.

<span class="mw-page-title-main">Major scale</span> Musical scale made of seven notes

The major scale is one of the most commonly used musical scales, especially in Western music. It is one of the diatonic scales. Like many musical scales, it is made up of seven notes: the eighth duplicates the first at double its frequency so that it is called a higher octave of the same note.

In music theory, a scale is "any consecutive series of notes that form a progression between one note and its octave", typically by order of pitch or fundamental frequency.

<span class="mw-page-title-main">Chromatic scale</span> Musical scale set of twelve pitches

The chromatic scale is a set of twelve pitches used in tonal music, with notes separated by the interval of a semitone. Chromatic instruments, such as the piano, are made to produce the chromatic scale, while other instruments capable of continuously variable pitch, such as the trombone and violin, can also produce microtones, or notes between those available on a piano.

<span class="mw-page-title-main">Music theory</span> Study of the practices and possibilities of music

Music theory is the study of theoretical frameworks for understanding the practices and possibilities of music. The Oxford Companion to Music describes three interrelated uses of the term "music theory": The first is the "rudiments", that are needed to understand music notation ; the second is learning scholars' views on music from antiquity to the present; the third is a sub-topic of musicology that "seeks to define processes and general principles in music". The musicological approach to theory differs from music analysis "in that it takes as its starting-point not the individual work or performance but the fundamental materials from which it is built."

<span class="mw-page-title-main">Anton Webern</span> Austrian composer and conductor (1883–1945)

Anton Webern was an Austrian composer, conductor, and musicologist. His music was among the most radical of its milieu in its concision and use of then novel atonal and twelve-tone techniques. His approach was typically rigorous, inspired by his studies of the Franco-Flemish School under Guido Adler and by Arnold Schoenberg's emphasis on structure in teaching composition from the music of Johann Sebastian Bach, the First Viennese School, and Johannes Brahms. Webern, Schoenberg, and their colleague Alban Berg were at the core of what became known as the Second Viennese School.

<span class="mw-page-title-main">Polytonality</span> Simultaneous use of multiple musical keys

Polytonality is the musical use of more than one key simultaneously. Bitonality is the use of only two different keys at the same time. Polyvalence or polyvalency is the use of more than one harmonic function, from the same key, at the same time.

In music, serialism is a method of composition using series of pitches, rhythms, dynamics, timbres or other musical elements. Serialism began primarily with Arnold Schoenberg's twelve-tone technique, though some of his contemporaries were also working to establish serialism as a form of post-tonal thinking. Twelve-tone technique orders the twelve notes of the chromatic scale, forming a row or series and providing a unifying basis for a composition's melody, harmony, structural progressions, and variations. Other types of serialism also work with sets, collections of objects, but not necessarily with fixed-order series, and extend the technique to other musical dimensions, such as duration, dynamics, and timbre.

<span class="mw-page-title-main">Twelve-tone technique</span> Musical composition method

The twelve-tone technique—also known as dodecaphony, twelve-tone serialism, and twelve-note composition—is a method of musical composition. The technique is a means of ensuring that all 12 notes of the chromatic scale are sounded equally often in a piece of music while preventing the emphasis of any one note through the use of tone rows, orderings of the 12 pitch classes. All 12 notes are thus given more or less equal importance, and the music avoids being in a key.

An octatonic scale is any eight-note musical scale. However, the term most often refers to the ancohemitonic symmetric scale composed of alternating whole and half steps, as shown at right. In classical theory, this symmetrical scale is commonly called the octatonic scale, although there are a total of 43 enharmonically inequivalent, transpositionally inequivalent eight-note sets.

<span class="mw-page-title-main">Circle of fifths</span> Relationship among tones of the chromatic scale

In music theory, the circle of fifths is a way of organizing pitches as a sequence of perfect fifths. Starting on a C, and using the standard system of tuning for Western music, the sequence is: C, G, D, A, E, B, F♯/G♭, C♯/D♭, G♯/A♭, D♯/E♭, A♯/B♭, F, and C. This order places the most closely related key signatures adjacent to one another.

In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave position." Important to musical set theory, a pitch class is "all pitches related to each other by octave, enharmonic equivalence, or both." Thus, using scientific pitch notation, the pitch class "C" is the set

Chromaticism is a compositional technique interspersing the primary diatonic pitches and chords with other pitches of the chromatic scale. In simple terms, within each octave, diatonic music uses only seven different notes, rather than the twelve available on a standard piano keyboard. Music is chromatic when it uses more than just these seven notes.

<span class="mw-page-title-main">Pandiatonicism</span>

Pandiatonicism is a musical technique of using the diatonic scale without the limitations of functional tonality. Music using this technique is pandiatonic.

<span class="mw-page-title-main">Consonance and dissonance</span> Categorizations of simultaneous or successive sounds

In music, consonance and dissonance are categorizations of simultaneous or successive sounds. Within the Western tradition, some listeners associate consonance with sweetness, pleasantness, and acceptability, and dissonance with harshness, unpleasantness, or unacceptability, although there is broad acknowledgement that this depends also on familiarity and musical expertise. The terms form a structural dichotomy in which they define each other by mutual exclusion: a consonance is what is not dissonant, and a dissonance is what is not consonant. However, a finer consideration shows that the distinction forms a gradation, from the most consonant to the most dissonant. In casual discourse, as German composer and music theorist Paul Hindemith stressed,

<span class="mw-page-title-main">Transformational theory</span> Branch of music theory

Transformational theory is a branch of music theory developed by David Lewin in the 1980s, and formally introduced in his 1987 work, Generalized Musical Intervals and Transformations. The theory—which models musical transformations as elements of a mathematical group—can be used to analyze both tonal and atonal music.

The Hungarian minor scale, double harmonic minor scale, or Gypsy minor scale is a type of combined musical scale. It is the same as the harmonic minor scale, except that it has a raised fourth scale degree to introduce an additional gap, or augmented second. It is a symmetrical scale with a slightly ambiguous tonal centre, due to the many half steps.

<span class="mw-page-title-main">Neo-Riemannian theory</span> Collection of ideas in music theory

Neo-Riemannian theory is a loose collection of ideas present in the writings of music theorists such as David Lewin, Brian Hyer, Richard Cohn, and Henry Klumpenhouwer. What binds these ideas is a central commitment to relating harmonies directly to each other, without necessary reference to a tonic. Initially, those harmonies were major and minor triads; subsequently, neo-Riemannian theory was extended to standard dissonant sonorities as well. Harmonic proximity is characteristically gauged by efficiency of voice leading. Thus, C major and E minor triads are close by virtue of requiring only a single semitonal shift to move from one to the other. Motion between proximate harmonies is described by simple transformations. For example, motion between a C major and E minor triad, in either direction, is executed by an "L" transformation. Extended progressions of harmonies are characteristically displayed on a geometric plane, or map, which portrays the entire system of harmonic relations. Where consensus is lacking is on the question of what is most central to the theory: smooth voice leading, transformations, or the system of relations that is mapped by the geometries. The theory is often invoked when analyzing harmonic practices within the Late Romantic period characterized by a high degree of chromaticism, including work of Schubert, Liszt, Wagner and Bruckner.

Dmitri Tymoczko is an American music theorist and composer. As a theorist, he has published more than two dozen articles dealing with topics related to contemporary tonality, including scales, voice leading, and functional harmonic norms. His article "The Geometry of Musical Chords" was the first music-theory article ever published by the journal Science. His music, which draws on rock, jazz, and romanticism, has been performed by ensembles such as the Amernet String Quartet, the Brentano Quartet, Janus, Newspeak, the San Francisco Contemporary Players, the Pacifica Quartet, and the pianist Ursula Oppens.

<span class="mw-page-title-main">Symphony (Webern)</span>

Symphony, Op. 21 was composed by Anton Webern between 1927 and 1928. It was his first twelve-tone orchestral work. The two-movement work lasts 10–20 minutes and is full of Alpine topics, abstraction, and intricate musical form, including some fixed register. The Symphony was influenced by Gustav Mahler. Alexander Smallens conducted the world premiere at New York's Town Hall on 18 December 1929.

References

Notes

  1. ↑ Cf. harmonic rhythm.
  2. ↑ In the music of many cultures, the pitch-class content is that of the pentatonic scale. [11]

Citations

  1. ↑ Gelbart 2019, 98n22; Hook 2011, 91; Newton 2019, 235; Scotto 2019, 262n3; Tymoczko 2011, 154.
  2. 1 2 Hook 2011, 91.
  3. ↑ Newton 2019, 235, 247n4; Tymoczko 2011, 15.
  4. ↑ Newton 2019, 235.
  5. ↑ Scotto 2019, 262n3.
  6. ↑ Scotto 2019, 262n3; Tymoczko 2011, 6n8.
  7. ↑ Tymoczko 2011, 3.
  8. ↑ Tymoczko 2011, 4.
  9. ↑ Tymoczko 2011, 3–5.
  10. 1 2 Tymoczko 2011, 154.
  11. 1 2 3 4 Gelbart 2019, 85, 98n22.
  12. ↑ Gelbart 2019, 98n22; Tymoczko 2011, 15, 121.

Bibliography

  • Gelbart, Matthew. 2019. "Scale". The Oxford Handbook of Critical Concepts in Music Theory, eds. and intro. Alexander Rehding and Steven Rings, 78–105. Oxford: Oxford University Press. ISBN   978-0-19-045474-6 (hbk).
  • Hook, Julian. 2011, June 15–17. "Spelled Heptachords". [Conference presentation]. Society for Mathematics and Computation in Music (Paris). Mathematics and Computation in Music 3, 84–97, eds. Carlos Agon, Emmanuel Amiot, Moreno Andreatta, Gérard Assayag, Jean Bresson, and John Mandereau. Berlin: Springer. ISBN   978-3-642-21590-2 (ebk). ISBN   978-3-642-21589-6 (pbk). doi:10.1007/978-3-642-21590-2_7.
  • Newton, Neil. 2019. "Chromatic Linear Progressions in Popular Music". The Routledge Companion to Popular Music Analysis: Expanding Approaches, eds. and intro. Ciro Scotto, Kenneth Smith, and John Brackett, 235–248. New York and London: Routledge. ISBN   978-1-138-68311-2 (hbk). ISBN   978-1-315-54470-0 (ebk).
  • Scotto, Ciro. 2019. "System 7". The Routledge Companion to Popular Music Analysis: Expanding Approaches, eds. and intro. Ciro Scotto, Kenneth Smith, and John Brackett, 249–264. New York and London: Routledge. ISBN   978-1-138-68311-2 (hbk). ISBN   978-1-315-54470-0 (ebk).
  • Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford Studies in Music Theory. Oxford: Oxford University Press, ed. Richard Cohn. ISBN   978-0-19-533667-2.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.