In quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function describes an electron's charge distribution around the atom's nucleus, and can be used to calculate the probability of finding an electron in a specific region around the nucleus.

A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral hydrogen atom contains a nucleus of a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.

In quantum physics, a wave function is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters ψ and Ψ. Wave functions are complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density of measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called normalization. Since the wave function is complex-valued, only its relative phase and relative magnitude can be measured; its value does not, in isolation, tell anything about the magnitudes or directions of measurable observables. One has to apply quantum operators, whose eigenvalues correspond to sets of possible results of measurements, to the wave function ψ and calculate the statistical distributions for measurable quantities.

In quantum mechanics, a spherically symmetric potential is a system of which the potential only depends on the radial distance from the spherical center and a location in space. A particle in a spherically symmetric potential will behave accordingly to said potential and can therefore be used as an approximation, for example, of the electron in a hydrogen atom or of the formation of chemical bonds.

In quantum physics and chemistry, quantum numbers are quantities that characterize the possible states of the system. To fully specify the state of the electron in a hydrogen atom, four quantum numbers are needed. The traditional set of quantum numbers includes the principal, azimuthal, magnetic, and spin quantum numbers. To describe other systems, different quantum numbers are required. For subatomic particles, one needs to introduce new quantum numbers, such as the flavour of quarks, which have no classical correspondence.
In quantum mechanics, the principal quantum number is one of four quantum numbers assigned to each electron in an atom to describe that electron's state. Its values are natural numbers making it a discrete variable.

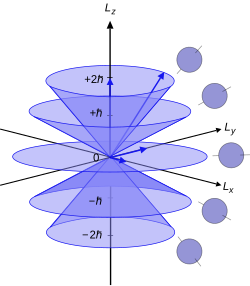
In quantum mechanics, the azimuthal quantum numberℓ is a quantum number for an atomic orbital that determines its orbital angular momentum and describes aspects of the angular shape of the orbital. The azimuthal quantum number is the second of a set of quantum numbers that describe the unique quantum state of an electron.
In quantum mechanics, a rotational transition is an abrupt change in angular momentum. Like all other properties of a quantum particle, angular momentum is quantized, meaning it can only equal certain discrete values, which correspond to different rotational energy states. When a particle loses angular momentum, it is said to have transitioned to a lower rotational energy state. Likewise, when a particle gains angular momentum, a positive rotational transition is said to have occurred.
In physics and chemistry, the spin quantum number is a quantum number that describes the intrinsic angular momentum of an electron or other particle. It has the same value for all particles of the same type, such as s = 1/2 for all electrons. It is an integer for all bosons, such as photons, and a half-odd-integer for all fermions, such as electrons and protons.
The old quantum theory is a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was instead a set of heuristic corrections to classical mechanics. The theory has come to be understood as the semi-classical approximation to modern quantum mechanics. The main and final accomplishments of the old quantum theory were the determination of the modern form of the periodic table by Edmund Stoner and the Pauli exclusion principle, both of which were premised on Arnold Sommerfeld's enhancements to the Bohr model of the atom.
In atomic physics, a term symbol is an abbreviated description of the total spin and orbital angular momentum quantum numbers of the electrons in a multi-electron atom. So while the word symbol suggests otherwise, it represents an actual value of a physical quantity.
In atomic physics, the electron magnetic moment, or more specifically the electron magnetic dipole moment, is the magnetic moment of an electron resulting from its intrinsic properties of spin and electric charge. The value of the electron magnetic moment is −9.2847646917(29)×10−24 J⋅T−1. In units of the Bohr magneton (μB), it is −1.00115965218059(13) μB, a value that was measured with a relative accuracy of 1.3×10−13.

Quantum orbital motion involves the quantum mechanical motion of rigid particles about some other mass, or about themselves. In classical mechanics, an object's orbital motion is characterized by its orbital angular momentum and spin angular momentum, which is the object's angular momentum about its own center of mass. In quantum mechanics there are analogous orbital and spin angular momenta which describe the orbital motion of a particle, represented as quantum mechanical operators instead of vectors.
In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry. Being an observable, its eigenfunctions represent the distinguishable physical states of a system's angular momentum, and the corresponding eigenvalues the observable experimental values. When applied to a mathematical representation of the state of a system, yields the same state multiplied by its angular momentum value if the state is an eigenstate. In both classical and quantum mechanical systems, angular momentum is one of the three fundamental properties of motion.
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-1/2 particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927. In its linearized form it is known as Lévy-Leblond equation.
A hydrogen-like atom (or hydrogenic atom) is any atom or ion with a single valence electron. These atoms are isoelectronic with hydrogen. Examples of hydrogen-like atoms include, but are not limited to, hydrogen itself, all alkali metals such as Rb and Cs, singly ionized alkaline earth metals such as Ca+ and Sr+ and other ions such as He+, Li2+, and Be3+ and isotopes of any of the above. A hydrogen-like atom includes a positively charged core consisting of the atomic nucleus and any core electrons as well as a single valence electron. Because helium is common in the universe, the spectroscopy of singly ionized helium is important in EUV astronomy, for example, of DO white dwarf stars.
Spin is an intrinsic form of angular momentum carried by elementary particles, and thus by composite particles such as hadrons, atomic nuclei, and atoms. Spin is quantized, and accurate models for the interaction with spin require relativistic quantum mechanics or quantum field theory.
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.

Electrons in free space can carry quantized orbital angular momentum (OAM) projected along the direction of propagation. This orbital angular momentum corresponds to helical wavefronts, or, equivalently, a phase proportional to the azimuthal angle. Electron beams with quantized orbital angular momentum are also called electron vortex beams.