 | The factual accuracy of part of this article is disputed. The dispute is about "26. A semi-modular lattice is atomic.".(May 2017) |
The concept of a lattice arises in order theory, a branch of mathematics. The Hasse diagram below depicts the inclusion relationships among some important subclasses of lattices.
| Algebraic structures |
|---|
1. A boolean algebra is a complemented distributive lattice. (def)
2. A boolean algebra is a heyting algebra. [1]
3. A boolean algebra is orthocomplemented. [2]
4. A distributive orthocomplemented lattice is orthomodular. [3]
5. A boolean algebra is orthomodular. (1,3,4)
6. An orthomodular lattice is orthocomplemented. (def)
7. An orthocomplemented lattice is complemented. (def)
8. A complemented lattice is bounded. (def)
9. An algebraic lattice is complete. (def)
10. A complete lattice is bounded.
11. A heyting algebra is bounded. (def)
12. A bounded lattice is a lattice. (def)
13. A heyting algebra is residuated.
14. A residuated lattice is a lattice. (def)
15. A distributive lattice is modular. [4]
16. A modular complemented lattice is relatively complemented. [5]
17. A boolean algebra is relatively complemented. (1,15,16)
18. A relatively complemented lattice is a lattice. (def)
19. A heyting algebra is distributive. [6]
20. A totally ordered set is a distributive lattice.
21. A metric lattice is modular. [7]
22. A modular lattice is semi-modular. [8]
23. A projective lattice is modular. [9]
24. A projective lattice is geometric. (def)
25. A geometric lattice is semi-modular. [10]
26. A semi-modular lattice is atomic. [11] [ disputed ]
27. An atomic lattice is a lattice. (def)
28. A lattice is a semi-lattice. (def)
29. A semi-lattice is a partially ordered set. (def)
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets, or its elements can be viewed as generalized truth values. It is also a special case of a De Morgan algebra and a Kleene algebra.
In mathematics, a Heyting algebra is a bounded lattice equipped with a binary operation a → b of implication such that ≤ b is equivalent to c ≤. From a logical standpoint, A → B is by this definition the weakest proposition for which modus ponens, the inference rule A → B, A ⊢ B, is sound. Like Boolean algebras, Heyting algebras form a variety axiomatizable with finitely many equations. Heyting algebras were introduced by Arend Heyting (1930) to formalize intuitionistic logic.
In mathematics, a distributive lattice is a lattice in which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to isomorphism—given as such a lattice of sets.
In mathematics, the Boolean prime ideal theorem states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on sets is known as the ultrafilter lemma. Other theorems are obtained by considering different mathematical structures with appropriate notions of ideals, for example, rings and prime ideals, or distributive lattices and maximal ideals. This article focuses on prime ideal theorems from order theory.
This is a glossary of some terms used in various branches of mathematics that are related to the fields of order, lattice, and domain theory. Note that there is a structured list of order topics available as well. Other helpful resources might be the following overview articles:
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum and a unique infimum. An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor.
In mathematical order theory, an ideal is a special subset of a partially ordered set (poset). Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion. Ideals are of great importance for many constructions in order and lattice theory.
In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set (poset). The most familiar example is the completeness of the real numbers. A special use of the term refers to complete partial orders or complete lattices. However, many other interesting notions of completeness exist.
In the mathematical area of order theory, there are various notions of the common concept of distributivity, applied to the formation of suprema and infima. Most of these apply to partially ordered sets that are at least lattices, but the concept can in fact reasonably be generalized to semilattices as well.
In the mathematical study of logic and the physical analysis of quantum foundations, quantum logic is a set of rules for manipulation of propositions inspired by the structure of quantum theory. The field takes as its starting point an observation of Garrett Birkhoff and John von Neumann, that the structure of experimental tests in classical mechanics forms a Boolean algebra, but the structure of experimental tests in quantum mechanics forms a much more complicated structure.
In the mathematical discipline of order theory, a complemented lattice is a bounded lattice, in which every element a has a complement, i.e. an element b satisfying a ∨ b = 1 and a ∧ b = 0. Complements need not be unique.
In abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y, loosely analogous to division or implication, when x•y is viewed as multiplication or conjunction, respectively. Called respectively right and left residuals, these operations coincide when the monoid is commutative. The general concept was introduced by Morgan Ward and Robert P. Dilworth in 1939. Examples, some of which existed prior to the general concept, include Boolean algebras, Heyting algebras, residuated Boolean algebras, relation algebras, and MV-algebras. Residuated semilattices omit the meet operation ∧, for example Kleene algebras and action algebras.
In mathematics, there are many types of algebraic structures which are studied. Abstract algebra is primarily the study of specific algebraic structures and their properties. Algebraic structures may be viewed in different ways, however the common starting point of algebra texts is that an algebraic object incorporates one or more sets with one or more binary operations or unary operations satisfying a collection of axioms.
Boolean algebra is a mathematically rich branch of abstract algebra. Stanford Encyclopaedia of Philosophy defines Boolean algebra as 'the algebra of two-valued logic with only sentential connectives, or equivalently of algebras of sets under union and complementation.' Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under some operations satisfying certain equations.
In mathematics, a De Morgan algebra is a structure A = (A, ∨, ∧, 0, 1, ¬) such that:
In mathematics, especially in the areas of abstract algebra known as universal algebra, group theory, ring theory, and module theory, a subdirect product is a subalgebra of a direct product that depends fully on all its factors without however necessarily being the whole direct product. The notion was introduced by Birkhoff in 1944 and has proved to be a powerful generalization of the notion of direct product.
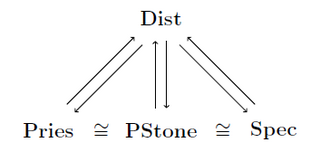
In mathematics, duality theory for distributive lattices provides three different representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces. This duality, which is originally also due to Marshall H. Stone, generalizes the well-known Stone duality between Stone spaces and Boolean algebras.
In mathematics, a Stone algebra, or Stone lattice, is a pseudo-complemented distributive lattice such that a* ∨ a** = 1. They were introduced by Grätzer & Schmidt (1957) and named after Marshall Harvey Stone.
In mathematics, particularly in order theory, a pseudocomplement is one generalization of the notion of complement. In a lattice L with bottom element 0, an element x ∈ L is said to have a pseudocomplement if there exists a greatest element x* ∈ L with the property that x ∧ x* = 0. More formally, x* = max{ y ∈ L | x ∧ y = 0 }. The lattice L itself is called a pseudocomplemented lattice if every element of L is pseudocomplemented. Every pseudocomplemented lattice is necessarily bounded, i.e. it has a 1 as well. Since the pseudocomplement is unique by definition, a pseudocomplemented lattice can be endowed with a unary operation * mapping every element to its pseudocomplement; this structure is sometimes called a p-algebra. However this latter term may have other meanings in other areas of mathematics.