In astronomy, declination is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle. The declination angle is measured north (positive) or south (negative) of the celestial equator, along the hour circle passing through the point in question.

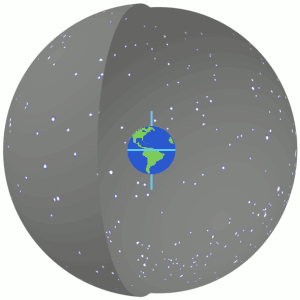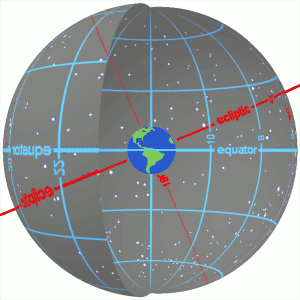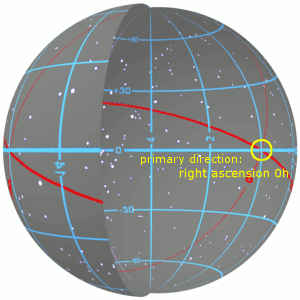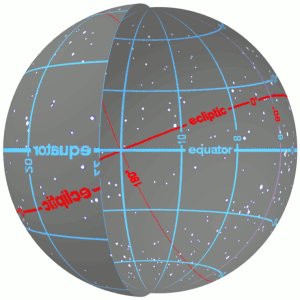
The ecliptic or ecliptic plane is the orbital plane of Earth around the Sun. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic against the background of stars. The ecliptic is an important reference plane and is the basis of the ecliptic coordinate system.

Right ascension is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the March equinox to the point in question above the Earth. When paired with declination, these astronomical coordinates specify the location of a point on the celestial sphere in the equatorial coordinate system.
A solstice is the time when the Sun reaches its most northerly or southerly excursion relative to the celestial equator on the celestial sphere. Two solstices occur annually, around 20–22 June and 20–22 December. In many countries, the seasons of the year are defined by reference to the solstices and the equinoxes.

The equatorial coordinate system is a celestial coordinate system widely used to specify the positions of celestial objects. It may be implemented in spherical or rectangular coordinates, both defined by an origin at the centre of Earth, a fundamental plane consisting of the projection of Earth's equator onto the celestial sphere, a primary direction towards the March equinox, and a right-handed convention.

In astronomy, the ecliptic coordinate system is a celestial coordinate system commonly used for representing the apparent positions, orbits, and pole orientations of Solar System objects. Because most planets and many small Solar System bodies have orbits with only slight inclinations to the ecliptic, using it as the fundamental plane is convenient. The system's origin can be the center of either the Sun or Earth, its primary direction is towards the March equinox, and it has a right-hand convention. It may be implemented in spherical or rectangular coordinates.

Orbital inclination measures the tilt of an object's orbit around a celestial body. It is expressed as the angle between a reference plane and the orbital plane or axis of direction of the orbiting object.

In astronomy, axial precession is a gravity-induced, slow, and continuous change in the orientation of an astronomical body's rotational axis. In the absence of precession, the astronomical body's orbit would show axial parallelism. In particular, axial precession can refer to the gradual shift in the orientation of Earth's axis of rotation in a cycle of approximately 26,000 years. This is similar to the precession of a spinning top, with the axis tracing out a pair of cones joined at their apices. The term "precession" typically refers only to this largest part of the motion; other changes in the alignment of Earth's axis—nutation and polar motion—are much smaller in magnitude.

In astronomy, an analemma is a diagram showing the position of the Sun in the sky as seen from a fixed location on Earth at the same mean solar time over the course of a year. The change of position is a result of the shifting of the angle in the sky of the path that the Sun takes in respect to the stars. The diagram resembles a figure eight. Globes of the Earth often display an analemma as a two-dimensional figure of equation of time vs. declination of the Sun.

The celestial equator is the great circle of the imaginary celestial sphere on the same plane as the equator of Earth. By extension, it is also a plane of reference in the equatorial coordinate system. In other words, the celestial equator is an abstract projection of the terrestrial equator into outer space. Due to Earth's axial tilt, the celestial equator is currently inclined by about 23.44° with respect to the ecliptic, but has varied from about 22.0° to 24.5° over the past 5 million years due to perturbation from other planets.
In observational astronomy, culmination is the passage of a celestial object across the observer's local meridian. These events are also known as meridian transits, used in timekeeping and navigation, and measured precisely using a transit telescope.

A lunar node is either of the two orbital nodes of the Moon, that is, the two points at which the orbit of the Moon intersects the ecliptic. The ascending node is where the Moon moves into the northern ecliptic hemisphere, while the descending node is where the Moon enters the southern ecliptic hemisphere.

Spherical astronomy, or positional astronomy, is a branch of observational astronomy used to locate astronomical objects on the celestial sphere, as seen at a particular date, time, and location on Earth. It relies on the mathematical methods of spherical trigonometry and the measurements of astrometry.
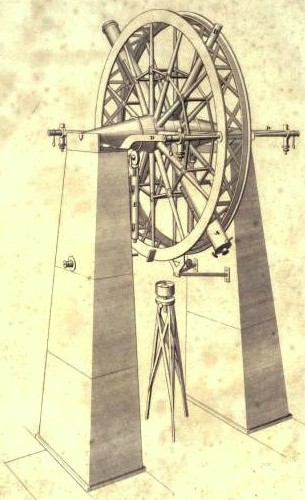
The meridian circle is an instrument for timing of the passage of stars across the local meridian, an event known as a culmination, while at the same time measuring their angular distance from the nadir. These are special purpose telescopes mounted so as to allow pointing only in the meridian, the great circle through the north point of the horizon, the north celestial pole, the zenith, the south point of the horizon, the south celestial pole, and the nadir. Meridian telescopes rely on the rotation of the sky to bring objects into their field of view and are mounted on a fixed, horizontal, east–west axis.

A lunar standstill or lunistice is when the Moon reaches its furthest north or furthest south point during the course of a month. The declination at lunar standstill varies in a cycle 18.6 years long between 18.134° and 28.725°, due to lunar precession. These extremes are called the minor and major lunar standstills.

The Moon orbits Earth in the prograde direction and completes one revolution relative to the Vernal Equinox and the stars in about 27.32 days and one revolution relative to the Sun in about 29.53 days. Earth and the Moon orbit about their barycentre, which lies about 4,670 km from Earth's centre, forming a satellite system called the Earth–Moon system. On average, the distance to the Moon is about 384,400 km (238,900 mi) from Earth's centre, which corresponds to about 60 Earth radii or 1.282 light-seconds.
The poles of astronomical bodies are determined based on their axis of rotation in relation to the celestial poles of the celestial sphere. Astronomical bodies include stars, planets, dwarf planets and small Solar System bodies such as comets and minor planets, as well as natural satellites and minor-planet moons.

Earth-centered inertial (ECI) coordinate frames have their origins at the center of mass of Earth and are fixed with respect to the stars. "I" in "ECI" stands for inertial, in contrast to the "Earth-centered – Earth-fixed" (ECEF) frames, which remains fixed with respect to Earth's surface in its rotation, and then rotates with respect to stars.
This glossary of astronomy is a list of definitions of terms and concepts relevant to astronomy and cosmology, their sub-disciplines, and related fields. Astronomy is concerned with the study of celestial objects and phenomena that originate outside the atmosphere of Earth. The field of astronomy features an extensive vocabulary and a significant amount of jargon.

The position of the Sun in the sky is a function of both the time and the geographic location of observation on Earth's surface. As Earth orbits the Sun over the course of a year, the Sun appears to move with respect to the fixed stars on the celestial sphere, along a circular path called the ecliptic.

















