Physical information

Last updated December 21, 2020

Physical information is a form of information. In physics, it refers to the information of a physical system. Physical information is an important concept used in a number of fields of study in physics. For example, in quantum mechanics, the form of physical information known as quantum information is used to describe quantum phenomena such as entanglement and superposition.^[1]^[2]^[3]^[4]^[5]^[6] In thermodynamics and statistical mechanics, the concept of physical information is likewise used to describe phenomena related to thermodynamic entropy. (See Entropy in thermodynamics and information theory for an overview of this subject). The concept of information is also important in relativity, since correlations between events in spacetime can be measured in terms of physical information.^[7]^[8]^[9]^[10]^[11]^[12]

In a general sense, information is that which resolves uncertainty about the state of a physical system at a given moment in time. Information can also be understood as a measure of probability as follows: a physical state with a low initial probability of observation contains a relatively high quantity of physical information, while a state with a high initial probability of observation contains a relatively low quantity of physical information.

When clarifying the subject of information, care should be taken to distinguish between the following specific cases:^{[ citation needed ]}

The phrase instance of information refers to the specific instantiation of information (identity, form, essence) that is associated with the being of a particular example of a thing. (This allows for the reference to separate instances of information that happen to share identical patterns.)
A holder of information is a variable or mutable instance that can have different forms at different times (or in different situations).
A piece of information is a particular fact about a thing's identity or properties, i.e., a portion of its instance.
A pattern of information (or form) is the pattern or content of an instance or piece of information. Many separate pieces of information may share the same form. We can say that those pieces are perfectly correlated or say that they are copies of each other, as in copies of a book.
An embodiment of information is the thing whose essence is a given instance of information.
A representation of information is an encoding of some pattern of information within some other pattern or instance.
An interpretation of information is a decoding of a pattern of information as being a representation of another specific pattern or fact.
A subject of information is the thing that is identified or described by a given instance or piece of information. (Most generally, a thing that is a subject of information could be either abstract or concrete; either mathematical or physical.)
An amount of information is a quantification of how large a given instance, piece, or pattern of information is, or how much of a given system's information content (its instance) has a given attribute, such as being known or unknown. Amounts of information are most naturally characterized in logarithmic units.

As the above usages are all conceptually distinct from each other, overloading the word "information" (by itself) to denote (or connote) several of these concepts simultaneously can lead to confusion. Accordingly, this article uses more detailed phrases, such as those shown in bold above, whenever the intended meaning is not made clear by the context.

Classical versus quantum information

The instance of information that is contained in a physical system is generally considered to specify that system's "true" state. (A realist would assert that a physical system always has a true state of some sort—whether classical or quantum—even though, in many practical situations, the system's true state may be largely unknown.)

When discussing the information that is contained in physical systems according to modern quantum physics, we must distinguish between classical information and quantum information. Quantum information specifies the complete quantum state vector (or equivalently, wavefunction) of a system, whereas classical information, roughly speaking, only picks out a definite (pure) quantum state if we are already given a prespecified set of distinguishable (orthogonal) quantum states to choose from; such a set forms a basis for the vector space of all the possible pure quantum states (see pure state). Quantum information could thus be expressed by providing (1) a choice of a basis such that the actual quantum state is equal to one of the basis vectors, together with (2) the classical information specifying which of these basis vectors is the actual one. (However, the quantum information by itself does not include a specification of the basis, indeed, an uncountable number of different bases will include any given state vector.)

Note that the amount of classical information in a quantum system gives the maximum amount of information that can actually be measured and extracted from that quantum system for use by external classical (decoherent) systems, since only basis states are operationally distinguishable from each other. The impossibility of differentiating between non-orthogonal states is a fundamental principle of quantum mechanics,^{[ citation needed ]} equivalent to Heisenberg's uncertainty principle.^{[ citation needed ]} Because of its more general utility, the remainder of this article will deal primarily with classical information, although quantum information theory does also have some potential applications (quantum computing, quantum cryptography, quantum teleportation) that are currently being actively explored by both theorists and experimentalists.^[13]

Quantifying classical physical information

An amount of (classical) physical information may be quantified, as in information theory, as follows.^[14] For a system S, defined abstractly in such a way that it has N distinguishable states (orthogonal quantum states) that are consistent with its description, the amount of information I(S) contained in the system's state can be said to be log(N). The logarithm is selected for this definition since it has the advantage that this measure of information content is additive when concatenating independent, unrelated subsystems; e.g., if subsystem A has N distinguishable states (I(A) = log(N) information content) and an independent subsystem B has M distinguishable states (I(B) = log(M) information content), then the concatenated system has NM distinguishable states and an information content I(AB) = log(NM) = log(N) + log(M) = I(A) + I(B). We expect information to be additive from our everyday associations with the meaning of the word, e.g., that two pages of a book can contain twice as much information as one page.

The base of the logarithm used in this definition is arbitrary, since it affects the result by only a multiplicative constant, which determines the unit of information that is implied. If the log is taken base 2, the unit of information is the binary digit or bit (so named by John Tukey); if we use a natural logarithm instead, we might call the resulting unit the "nat." In magnitude, a nat is apparently identical to Boltzmann's constant k or the ideal gas constant R, although these particular quantities are usually reserved to measure physical information that happens to be entropy, and that are expressed in physical units such as joules per kelvin, or kilocalories per mole-kelvin.

Physical information and entropy

An easy way to understand the underlying unity between physical (as in thermodynamic) entropy and information-theoretic entropy is as follows:

Entropy is simply that portion of the (classical) physical information contained in a system of interest (whether it is an entire physical system, or just a subsystem delineated by a set of possible messages) whose identity (as opposed to amount) is unknown (from the point of view of a particular knower).

This informal characterization corresponds to both von Neumann's formal definition of the entropy of a mixed quantum state (which is just a statistical mixture of pure states; see von Neumann entropy), as well as Claude Shannon's definition of the entropy of a probability distribution over classical signal states or messages (see information entropy).^[14] Incidentally, the credit for Shannon's entropy formula (though not for its use in an information theory context) really belongs to Boltzmann, who derived it much earlier for use in his H-theorem of statistical mechanics.^[15] (Shannon himself references Boltzmann in his monograph.^[14])

Furthermore, even when the state of a system is known, we can say that the information in the system is still effectively entropy if that information is effectively incompressible, that is, if there are no known or feasibly determinable correlations or redundancies between different pieces of information within the system. Note that this definition of entropy can even be viewed as equivalent to the previous one (unknown information) if we take a meta-perspective, and say that for observer A to "know" the state of system B means simply that there is a definite correlation between the state of observer A and the state of system B; this correlation could thus be used by a meta-observer (that is, whoever is discussing the overall situation regarding A's state of knowledge about B) to compress his own description of the joint system AB.^[16]

Due to this connection with algorithmic information theory,^[17] entropy can be said to be that portion of a system's information capacity which is "used up," that is, unavailable for storing new information (even if the existing information content were to be compressed). The rest of a system's information capacity (aside from its entropy) might be called extropy, and it represents the part of the system's information capacity which is potentially still available for storing newly derived information. The fact that physical entropy is basically "used-up storage capacity" is a direct concern in the engineering of computing systems; e.g., a computer must first remove the entropy from a given physical subsystem (eventually expelling it to the environment, and emitting heat) in order for that subsystem to be used to store some newly computed information.^[16]

Extreme physical information

In a theory developed by B. Roy Frieden,^[18]^[19]^[20]^[21] "physical information" is defined as the loss of Fisher information that is incurred during the observation of a physical effect. Thus, if the effect has an intrinsic information level J but is observed at information level I, the physical information is defined to be the difference I−J. Because I and J are functionals, this difference defines an informational Lagrangian. Frieden's principle of extreme physical information (EPI), which is analogous to the principle of stationary action, states that minimizing the quantity I−J yields equations that correctly describe the evolution of a given physical system over time. However, the EPI principle has been met with considerable criticism within the scientific community.^[22] The EPI principle should not be confused with the more conventional principle of maximum entropy used in maximum entropy thermodynamics.

Related Research Articles

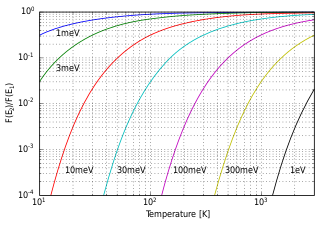
In statistical mechanics and mathematics, a Boltzmann distribution is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system. The distribution is expressed in the form:

Entropy is a scientific concept, as well as a measurable physical property that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far ranging applications in chemistry and physics, biological systems and their relation to life, cosmology, economics, sociology, weather science and climate change, and information systems and the transmission of information in telecommunication.

The holographic principle is a tenet of string theories and a supposed property of quantum gravity that states that the description of a volume of space can be thought of as encoded on a lower-dimensional boundary to the region—such as a light-like boundary like a gravitational horizon. First proposed by Gerard 't Hooft, it was given a precise string-theory interpretation by Leonard Susskind, who combined his ideas with previous ones of 't Hooft and Charles Thorn. As pointed out by Raphael Bousso, Thorn observed in 1978 that string theory admits a lower-dimensional description in which gravity emerges from it in what would now be called a holographic way. The prime example of holography is the AdS/CFT correspondence.

Quantum information is the information of the state of a quantum system. It is the basic entity of study in quantum information theory, and can be manipulated using quantum information processing techniques. Quantum information refers to both the technical definition in terms of Von Neumann entropy and the general computational term.

Statistical mechanics, one of the pillars of modern physics, describes how macroscopic observations are related to microscopic parameters that fluctuate around an average. It connects thermodynamic quantities to microscopic behavior, whereas, in classical thermodynamics, the only available option would be to measure and tabulate such quantities for various materials.

Statistical physics is a branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic nature. Its applications include many problems in the fields of physics, biology, chemistry, neuroscience, and even some social sciences, such as sociology and linguistics. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion.

The second law of thermodynamics establishes the concept of entropy as a physical property of a thermodynamic system. Entropy predicts the direction of spontaneous processes, and determines whether they are irreversible or impossible, despite obeying the requirement of conservation of energy, which is established in the first law of thermodynamics. The second law may be formulated by the observation that the entropy of isolated systems left to spontaneous evolution cannot decrease, as they always arrive at a state of thermodynamic equilibrium, where the entropy is highest. If all processes in the system are reversible, the entropy is constant.

T-symmetry Time reversal symmetry in physics

In physics, T-symmetry or time reversal symmetry is the study of the symmetry of physical laws under the inversion of the flow of the direction of time. It is a very active area of study, as there currently appears to be an unresolved paradox between the known microscopic and macroscopic laws of physics. In particular, most of the microscopic laws, those that govern atomic physics and particle physics, appear to be fully symmetric under time reversal. By contrast, at the human scale, time obviously flows in only one direction: from past to future, and never in reverse. Thus, a fundamental task is to understand how time-symmetric microscopic laws lead to time-asymmetric macroscopic laws. Aside from this, the study of T-symmetry also includes the careful articulation of the specific symmetry of specific laws and formulas.

In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually consists of all possible values of position and momentum variables. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs.

In classical statistical mechanics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the tendency to decrease in the quantity H in a nearly-ideal gas of molecules. As this quantity H was meant to represent the entropy of thermodynamics, the H-theorem was an early demonstration of the power of statistical mechanics as it claimed to derive the second law of thermodynamics—a statement about fundamentally irreversible processes—from reversible microscopic mechanics. It is thought to prove the second law of thermodynamics, albeit under the assumption of low-entropy initial conditions.

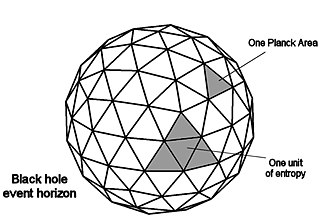
In physics, the Bekenstein bound is an upper limit on the entropy S, or information I, that can be contained within a given finite region of space which has a finite amount of energy—or conversely, the maximal amount of information required to perfectly describe a given physical system down to the quantum level. It implies that the information of a physical system, or the information necessary to perfectly describe that system, must be finite if the region of space and the energy is finite. In computer science, this implies that there is a maximal information-processing rate for a physical system that has a finite size and energy, and that a Turing machine with finite physical dimensions and unbounded memory is not physically possible.

In quantum statistical mechanics, the von Neumann entropy, named after John von Neumann, is the extension of classical Gibbs entropy concepts to the field of quantum mechanics. For a quantum-mechanical system described by a density matrix $ρ$ , the von Neumann entropy is

In physics, maximum entropy thermodynamics views equilibrium thermodynamics and statistical mechanics as inference processes. More specifically, MaxEnt applies inference techniques rooted in Shannon information theory, Bayesian probability, and the principle of maximum entropy. These techniques are relevant to any situation requiring prediction from incomplete or insufficient data. MaxEnt thermodynamics began with two papers by Edwin T. Jaynes published in the 1957 Physical Review.

Landauer's principle is a physical principle pertaining to the lower theoretical limit of energy consumption of computation. It holds that "any logically irreversible manipulation of information, such as the erasure of a bit or the merging of two computation paths, must be accompanied by a corresponding entropy increase in non-information-bearing degrees of freedom of the information-processing apparatus or its environment".

The mathematical expressions for thermodynamic entropy in the statistical thermodynamics formulation established by Ludwig Boltzmann and J. Willard Gibbs in the 1870s are similar to the information entropy by Claude Shannon and Ralph Hartley, developed in the 1940s.

The concept entropy was first developed by German physicist Rudolf Clausius in the mid-nineteenth century as a thermodynamic property that predicts that certain spontaneous processes are irreversible or impossible. In statistical mechanics, entropy is formulated as a statistical property using probability theory. The statistical entropy perspective was introduced in 1870 by Austrian physicist Ludwig Boltzmann, who established a new field of physics that provided the descriptive linkage between the macroscopic observation of nature and the microscopic view based on the rigorous treatment of a large ensembles of microstates that constitute thermodynamic systems.

In thermodynamics, entropy is a numerical quantity that shows that many physical processes can go in only one direction in time. For example, you can pour cream into coffee and mix it, but you cannot "unmix" it; you can burn a piece of wood, but you can't "unburn" it. The word 'entropy' has entered popular usage to refer a lack of order or predictability, or of a gradual decline into disorder. A more physical interpretation of thermodynamic entropy refers to spread of energy or matter, or to extent and diversity of microscopic motion.

Temperature Physical quantity that expresses hot and cold

Temperature is a physical quantity that expresses hot and cold. It is the manifestation of thermal energy, present in all matter, which is the source of the occurrence of heat, a flow of energy, when a body is in contact with another that is colder.

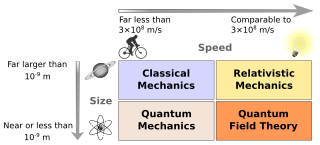
Physics deals with the combination of matter and energy. It also deals with a wide variety of systems, about which theories have been developed that are used by physicists. In general, theories are experimentally tested numerous times before they are accepted as correct as a description of Nature. For instance, the theory of classical mechanics accurately describes the motion of objects, provided they are much larger than atoms and moving at much less than the speed of light. These "central theories" are important tools for research in more specialized topics, and any physicist, regardless of his or her specialization, is expected to be literate in them.

In information theory, the principle of minimum Fisher information (MFI) is a variational principle which, when applied with the proper constraints needed to reproduce empirically known expectation values, determines the best probability distribution that characterizes the system.

References

↑ Vedral, Vlatko. (2018). Decoding Reality : The Universe as Quantum Information. Oxford University Press. ISBN 978-0-19-881543-3. OCLC 1038430295.
↑ Entangled world : the fascination of quantum information and computation. Audretsch, Jürgen, 1942-. Weinheim: Wiley-VCH. 2006. ISBN 978-3-527-61909-2. OCLC 212178399.CS1 maint: others (link)
↑ Schumacher, Benjamin. (2010). Quantum processes, systems, and information. Westmoreland, Michael D. New York: Cambridge University Press. ISBN 978-0-511-67753-3. OCLC 663882708.
↑ Khrennikov, Andrei (July 2016). "Reflections on Zeilinger-Brukner information interpretation of quantum mechanics". Foundations of Physics. 46 (7): 836–844. arXiv: 1512.07976 . Bibcode:2016FoPh...46..836K. doi:10.1007/s10701-016-0005-z. ISSN 0015-9018. S2CID 119267791.
↑ Lloyd, Seth, 1960- (2006). Programming the universe : a quantum computer scientist takes on the cosmos (1st ed.). New York: Knopf. ISBN 1-4000-4092-2. OCLC 60515043.CS1 maint: multiple names: authors list (link)
↑ Susskind, Leonard (25 February 2014). Quantum mechanics : the theoretical minimum. Friedman, Art. New York. ISBN 978-0-465-03667-7. OCLC 853310551.
↑ Glattfelder, James B. (2019), Glattfelder, James B. (ed.), "A Universe Built of Information", Information—Consciousness—Reality: How a New Understanding of the Universe Can Help Answer Age-Old Questions of Existence, The Frontiers Collection, Cham: Springer International Publishing, pp. 473–514, doi:10.1007/978-3-030-03633-1_13, ISBN 978-3-030-03633-1 , retrieved 2020-11-01
↑ Peres, Asher; Terno, Daniel R. (2004-01-06). "Quantum information and relativity theory". Reviews of Modern Physics. 76 (1): 93–123. arXiv: quant-ph/0212023 . Bibcode:2004RvMP...76...93P. doi:10.1103/RevModPhys.76.93. S2CID 7481797.
↑ Wheeler, John Archibald (1989), "Information, Physics, Quantum: The Search for Links", Proceedings III International Symposium on Foundations of Quantum Mechanics, pp. 354–358, retrieved 2020-11-01
↑ Moskowitz, Clara. "Tangled Up in Spacetime". Scientific American. Retrieved 2020-11-01.
↑ Cowen, Ron (2015-11-19). "The quantum source of space-time". Nature News. 527 (7578): 290–293. Bibcode:2015Natur.527..290C. doi:10.1038/527290a. PMID 26581274. S2CID 4447880.
↑ "ShieldSquare Captcha". iopscience.iop.org. Retrieved 2020-11-01.
↑ Michael A. Nielsen and Isaac L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, 2000.
1 2 3 Claude E. Shannon and Warren Weaver, Mathematical Theory of Communication, University of Illinois Press, 1963.
↑ Carlo Cercignani, Ludwig Boltzmann: The Man Who Trusted Atoms, Oxford University Press, 1998.
1 2 Michael P. Frank, "Physical Limits of Computing", Computing in Science and Engineering, 4(3):16-25, May/June 2002. http://www.cise.ufl.edu/research/revcomp/physlim/plpaper.html
↑ W. H. Zurek, "Algorithmic randomness, physical entropy, measurements, and the demon of choice," in (Hey 1999), pp. 393-410, and reprinted in (Leff & Rex 2003), pp. 264-281.
↑ Frieden, B. Roy; Gatenby, Robert A. (2005-09-01). "Power laws of complex systems from extreme physical information". Physical Review E. 72 (3): 036101. arXiv: q-bio/0507011 . Bibcode:2005PhRvE..72c6101F. doi:10.1103/physreve.72.036101. ISSN 1539-3755. PMID 16241509. S2CID 17987848.
↑ Frieden, B. Roy; Soffer, Bernard H. (2006-11-16). "Information-theoretic significance of the Wigner distribution". Physical Review A. 74 (5): 052108. arXiv: quant-ph/0609157 . Bibcode:2006PhRvA..74e2108F. doi:10.1103/physreva.74.052108. ISSN 1050-2947. S2CID 55541671.
↑ Frieden, B. Roy; Soffer, Bernard H. (1995-09-01). "Lagrangians of physics and the game of Fisher-information transfer". Physical Review E. 52 (3): 2274–2286. Bibcode:1995PhRvE..52.2274F. doi:10.1103/physreve.52.2274. ISSN 1063-651X. PMID 9963668.
↑ B. Roy Frieden, Science from Fisher Information, Cambridge University Press, 2004.
↑ Lavis, D. A.; Streater, R. F. (2002-06-01). "Physics from Fisher information". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 33 (2): 327–343. doi:10.1016/S1355-2198(02)00007-2. ISSN 1355-2198.