Radiosity (radiometry)

Radiosity
Radiosity
Common symbols
SI unit	W·m−2
Other units	erg·cm−2·s−1
Dimension	MT−3

Last updated December 15, 2023

In radiometry, radiosity is the radiant flux leaving (emitted, reflected and transmitted by) a surface per unit area, and spectral radiosity is the radiosity of a surface per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength.^[1] The SI unit of radiosity is the watt per square metre (W/m²), while that of spectral radiosity in frequency is the watt per square metre per hertz (W·m⁻²·Hz⁻¹) and that of spectral radiosity in wavelength is the watt per square metre per metre (W·m⁻³)—commonly the watt per square metre per nanometre (W·m⁻²·nm⁻¹). The CGS unit erg per square centimeter per second (erg·cm⁻²·s⁻¹) is often used in astronomy. Radiosity is often called intensity^[2] in branches of physics other than radiometry, but in radiometry this usage leads to confusion with radiant intensity.

Mathematical definitions

Radiosity

Radiosity of a surface, denoted J_e ("e" for "energetic", to avoid confusion with photometric quantities), is defined as^[3]

J_{\mathrm {e} }={\frac {\partial \Phi _{\mathrm {e} }}{\partial A}}=J_{\mathrm {e,em} }+J_{\mathrm {e,r} }+J_{\mathrm {e,tr} },

where

∂ is the partial derivative symbol
$\Phi _{e}$ is the radiant flux leaving (emitted, reflected and transmitted)
$A$ is the area
$J_{e,em}=M_{e}$ is the emitted component of the radiosity of the surface, that is to say its exitance
$J_{e,r}$ is the reflected component of the radiosity of the surface
$J_{e,tr}$ is the transmitted component of the radiosity of the surface

For an opaque surface, the transmitted component of radiosity J_e,tr vanishes and only two components remain:

J_{\mathrm {e} }=M_{\mathrm {e} }+J_{\mathrm {e,r} }.

In heat transfer, combining these two factors into one radiosity term helps in determining the net energy exchange between multiple surfaces.

Spectral radiosity

Spectral radiosity in frequency of a surface, denoted J_e,ν, is defined as^[3]

J_{\mathrm {e} ,\nu }={\frac {\partial J_{\mathrm {e} }}{\partial \nu }},

where ν is the frequency.

Spectral radiosity in wavelength of a surface, denoted J_e,λ, is defined as^[3]

J_{\mathrm {e} ,\lambda }={\frac {\partial J_{\mathrm {e} }}{\partial \lambda }},

where λ is the wavelength.

Radiosity method

The two radiosity components of an opaque surface. Radiosity23.png — The two radiosity components of an opaque surface.

The radiosity of an opaque, gray and diffuse surface is given by

J_{\mathrm {e} }=M_{\mathrm {e} }+J_{\mathrm {e,r} }=\varepsilon \sigma T^{4}+(1-\varepsilon )E_{\mathrm {e} },

where

ε is the emissivity of that surface;
σ is the Stefan–Boltzmann constant;
T is the temperature of that surface;
E_e is the irradiance of that surface.

Normally, E_e is the unknown variable and will depend on the surrounding surfaces. So, if some surface i is being hit by radiation from some other surface j, then the radiation energy incident on surface i is E_e,jiA_i = F_jiA_jJ_e,j where F_ji is the view factor or shape factor, from surface j to surface i. So, the irradiance of surface i is the sum of radiation energy from all other surfaces per unit surface of area A_i:

E_{\mathrm {e} ,i}={\frac {\sum _{j=1}^{N}F_{ji}A_{j}J_{\mathrm {e} ,j}}{A_{i}}}.

Now, employing the reciprocity relation for view factors F_jiA_j = F_ijA_i,

E_{\mathrm {e} ,i}=\sum _{j=1}^{N}F_{ij}J_{\mathrm {e} ,j},

and substituting the irradiance into the equation for radiosity, produces

J_{\mathrm {e} ,i}=\varepsilon _{i}\sigma T_{i}^{4}+(1-\varepsilon _{i})\sum _{j=1}^{N}F_{ij}J_{\mathrm {e} ,j}.

For an N surface enclosure, this summation for each surface will generate N linear equations with N unknown radiosities,^[4] and N unknown temperatures. For an enclosure with only a few surfaces, this can be done by hand. But, for a room with many surfaces, linear algebra and a computer are necessary.

Once the radiosities have been calculated, the net heat transfer ${\dot {Q}}_{i}$ at a surface can be determined by finding the difference between the incoming and outgoing energy:

{\dot {Q}}_{i}=A_{i}\left(J_{\mathrm {e} ,i}-E_{\mathrm {e} ,i}\right).

Using the equation for radiosity J_e,i = ε_iσT_i⁴ + (1 − ε_i)E_e,i, the irradiance can be eliminated from the above to obtain

{\dot {Q}}_{i}={\frac {A_{i}\varepsilon _{i}}{1-\varepsilon _{i}}}\left(\sigma T_{i}^{4}-J_{\mathrm {e} ,i}\right)={\frac {A_{i}\varepsilon _{i}}{1-\varepsilon _{i}}}\left(M_{\mathrm {e} ,i}^{\circ }-J_{\mathrm {e} ,i}\right),

where M_e,i° is the radiant exitance of a black body.

Circuit analogy

For an enclosure consisting of only a few surfaces, it is often easier to represent the system with an analogous circuit rather than solve the set of linear radiosity equations. To do this, the heat transfer at each surface is expressed as

{\dot {Q_{i}}}={\frac {M_{\mathrm {e} ,i}^{\circ }-J_{\mathrm {e} ,i}}{R_{i}}},

where R_i = (1 − ε_i)/(A_iε_i) is the resistance of the surface.

Likewise, M_e,i^° − J_e,i is the blackbody exitance minus the radiosity and serves as the 'potential difference'. These quantities are formulated to resemble those from an electrical circuit V = IR.

Now performing a similar analysis for the heat transfer from surface i to surface j,

{\dot {Q}}_{ij}=A_{i}F_{ij}(J_{\mathrm {e} ,i}-J_{\mathrm {e} ,j})={\frac {J_{\mathrm {e} ,i}-J_{\mathrm {e} ,j}}{R_{ij}}},

where R_ij = 1/(A_iF_ij).

Because the above is between surfaces, R_ij is the resistance of the space between the surfaces and J_e,i − J_e,j serves as the potential difference.

Combining the surface elements and space elements, a circuit is formed. The heat transfer is found by using the appropriate potential difference and equivalent resistances, similar to the process used in analyzing electrical circuits.

Other methods

In the radiosity method and circuit analogy, several assumptions were made to simplify the model. The most significant is that the surface is a diffuse emitter. In such a case, the radiosity does not depend on the angle of incidence of reflecting radiation and this information is lost on a diffuse surface. In reality, however, the radiosity will have a specular component from the reflected radiation. So, the heat transfer between two surfaces relies on both the view factor and the angle of reflected radiation.

It was also assumed that the surface is a gray body, that is to say its emissivity is independent of radiation frequency or wavelength. However, if the range of radiation spectrum is large, this will not be the case. In such an application, the radiosity must be calculated spectrally and then integrated over the range of radiation spectrum.

Yet another assumption is that the surface is isothermal. If it is not, then the radiosity will vary as a function of position along the surface. However, this problem is solved by simply subdividing the surface into smaller elements until the desired accuracy is obtained.^[4]

SI radiometry units

SI radiometry units
v
t
e
Quantity		Unit		Dimension	Notes
Name	Symbol^{[nb 1]}	Name	Symbol	Dimension	Notes
Radiant energy	$Q e$ ^{[nb 2]}	joule	J	M⋅L²⋅T⁻²	Energy of electromagnetic radiation.
Radiant energy density	$w e$	joule per cubic metre	J/m³	M⋅L⁻¹⋅T⁻²	Radiant energy per unit volume.
Radiant flux	$Φ e$ ^{[nb 2]}	watt	W = J/s	M⋅L²⋅T⁻³	Radiant energy emitted, reflected, transmitted or received, per unit time. This is sometimes also called "radiant power", and called luminosity in Astronomy.
Spectral flux	$Φ e, ν$ ^{[nb 3]}	watt per hertz	W/Hz	M⋅L²⋅T⁻²	Radiant flux per unit frequency or wavelength. The latter is commonly measured in W⋅nm⁻¹.
Spectral flux	$Φ e, λ$ ^{[nb 4]}	watt per metre	W/m	M⋅L⋅T⁻³
Radiant intensity	$I e,Ω$ ^{[nb 5]}	watt per steradian	W/sr	M⋅L²⋅T⁻³	Radiant flux emitted, reflected, transmitted or received, per unit solid angle. This is a directional quantity.
Spectral intensity	$I e,Ω, ν$ ^{[nb 3]}	watt per steradian per hertz	W⋅sr⁻¹⋅Hz⁻¹	M⋅L²⋅T⁻²	Radiant intensity per unit frequency or wavelength. The latter is commonly measured in W⋅sr⁻¹⋅nm⁻¹. This is a directional quantity.
Spectral intensity	$I e,Ω, λ$ ^{[nb 4]}	watt per steradian per metre	W⋅sr⁻¹⋅m⁻¹	M⋅L⋅T⁻³
Radiance	$L e,Ω$ ^{[nb 5]}	watt per steradian per square metre	W⋅sr⁻¹⋅m⁻²	M⋅T⁻³	Radiant flux emitted, reflected, transmitted or received by a surface, per unit solid angle per unit projected area. This is a directional quantity. This is sometimes also confusingly called "intensity".
Spectral radiance Specific intensity	$L e,Ω, ν$ ^{[nb 3]}	watt per steradian per square metre per hertz	W⋅sr⁻¹⋅m⁻²⋅Hz⁻¹	M⋅T⁻²	Radiance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅sr⁻¹⋅m⁻²⋅nm⁻¹. This is a directional quantity. This is sometimes also confusingly called "spectral intensity".
Spectral radiance Specific intensity	$L e,Ω, λ$ ^{[nb 4]}	watt per steradian per square metre, per metre	W⋅sr⁻¹⋅m⁻³	M⋅L⁻¹⋅T⁻³
Irradiance Flux density	$E e$ ^{[nb 2]}	watt per square metre	W/m²	M⋅T⁻³	Radiant flux received by a surface per unit area. This is sometimes also confusingly called "intensity".
Spectral irradiance Spectral flux density	$E e, ν$ ^{[nb 3]}	watt per square metre per hertz	W⋅m⁻²⋅Hz⁻¹	M⋅T⁻²	Irradiance of a surface per unit frequency or wavelength. This is sometimes also confusingly called "spectral intensity". Non-SI units of spectral flux density include jansky (1 Jy = 10⁻²⁶ W⋅m⁻²⋅Hz⁻¹) and solar flux unit (1 sfu = 10⁻²² W⋅m⁻²⋅Hz⁻¹ = 10⁴ Jy).
Spectral irradiance Spectral flux density	$E e, λ$ ^{[nb 4]}	watt per square metre, per metre	W/m³	M⋅L⁻¹⋅T⁻³
Radiosity	$J e$ ^{[nb 2]}	watt per square metre	W/m²	M⋅T⁻³	Radiant flux leaving (emitted, reflected and transmitted by) a surface per unit area. This is sometimes also confusingly called "intensity".
Spectral radiosity	$J e, ν$ ^{[nb 3]}	watt per square metre per hertz	W⋅m⁻²⋅Hz⁻¹	M⋅T⁻²	Radiosity of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m⁻²⋅nm⁻¹. This is sometimes also confusingly called "spectral intensity".
Spectral radiosity	$J e, λ$ ^{[nb 4]}	watt per square metre, per metre	W/m³	M⋅L⁻¹⋅T⁻³
Radiant exitance	$M e$ ^{[nb 2]}	watt per square metre	W/m²	M⋅T⁻³	Radiant flux emitted by a surface per unit area. This is the emitted component of radiosity. "Radiant emittance" is an old term for this quantity. This is sometimes also confusingly called "intensity".
Spectral exitance	$M e, ν$ ^{[nb 3]}	watt per square metre per hertz	W⋅m⁻²⋅Hz⁻¹	M⋅T⁻²	Radiant exitance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m⁻²⋅nm⁻¹. "Spectral emittance" is an old term for this quantity. This is sometimes also confusingly called "spectral intensity".
Spectral exitance	$M e, λ$ ^{[nb 4]}	watt per square metre, per metre	W/m³	M⋅L⁻¹⋅T⁻³
Radiant exposure	$H e$	joule per square metre	J/m²	M⋅T⁻²	Radiant energy received by a surface per unit area, or equivalently irradiance of a surface integrated over time of irradiation. This is sometimes also called "radiant fluence".
Spectral exposure	$H e, ν$ ^{[nb 3]}	joule per square metre per hertz	J⋅m⁻²⋅Hz⁻¹	M⋅T⁻¹	Radiant exposure of a surface per unit frequency or wavelength. The latter is commonly measured in J⋅m⁻²⋅nm⁻¹. This is sometimes also called "spectral fluence".
Spectral exposure	$H e, λ$ ^{[nb 4]}	joule per square metre, per metre	J/m³	M⋅L⁻¹⋅T⁻²
See also: SI Radiometry Photometry

↑ Standards organizations recommend that radiometric quantities should be denoted with suffix "e" (for "energetic") to avoid confusion with photometric or photon quantities.
1 2 3 4 5 Alternative symbols sometimes seen: $W$ or $E$ for radiant energy, $P$ or $F$ for radiant flux, $I$ for irradiance, $W$ for radiant exitance.
1 2 3 4 5 6 7 Spectral quantities given per unit frequency are denoted with suffix " ν " (Greek letter nu, not to be confused with a letter "v", indicating a photometric quantity.)
1 2 3 4 5 6 7 Spectral quantities given per unit wavelength are denoted with suffix " λ ".
1 2 Directional quantities are denoted with suffix "Ω".

Related Research Articles

In physics, optical depth or optical thickness is the natural logarithm of the ratio of incident to transmitted radiant power through a material. Thus, the larger the optical depth, the smaller the amount of transmitted radiant power through the material. Spectral optical depth or spectral optical thickness is the natural logarithm of the ratio of incident to transmitted spectral radiant power through a material. Optical depth is dimensionless, and in particular is not a length, though it is a monotonically increasing function of optical path length, and approaches zero as the path length approaches zero. The use of the term "optical density" for optical depth is discouraged.

Radiometry is a set of techniques for measuring electromagnetic radiation, including visible light. Radiometric techniques in optics characterize the distribution of the radiation's power in space, as opposed to photometric techniques, which characterize the light's interaction with the human eye. The fundamental difference between radiometry and photometry is that radiometry gives the entire optical radiation spectrum, while photometry is limited to the visible spectrum. Radiometry is distinct from quantum techniques such as photon counting.

<span class="mw-page-title-main">Reflectance</span> Capacity of an object to reflect light

The reflectance of the surface of a material is its effectiveness in reflecting radiant energy. It is the fraction of incident electromagnetic power that is reflected at the boundary. Reflectance is a component of the response of the electronic structure of the material to the electromagnetic field of light, and is in general a function of the frequency, or wavelength, of the light, its polarization, and the angle of incidence. The dependence of reflectance on the wavelength is called a reflectance spectrum or spectral reflectance curve.

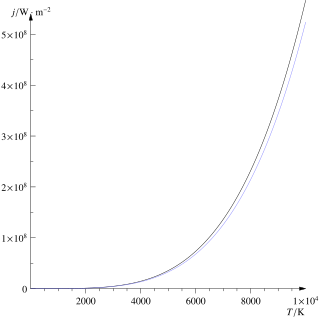
The Stefan–Boltzmann law, also known as Stefan's law, describes the intensity of the thermal radiation emitted by matter in terms of that matter's temperature. It is named for Josef Stefan, who empirically derived the relationship, and Ludwig Boltzmann who derived the law theoretically.

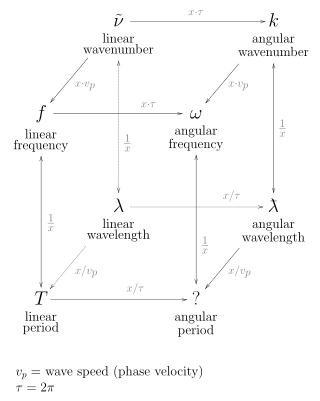
In the physical sciences, the wavenumber, also known as repetency, is the spatial frequency of a wave, measured in cycles per unit distance or radians per unit distance. It is analogous to temporal frequency, which is defined as the number of wave cycles per unit time or radians per unit time.

Thermal radiation is electromagnetic radiation generated by the thermal motion of particles in matter. Thermal radiation is generated when heat from the movement of charges in the material is converted to electromagnetic radiation. All matter with a temperature greater than absolute zero emits thermal radiation. At room temperature, most of the emission is in the infrared (IR) spectrum. Particle motion results in charge-acceleration or dipole oscillation which produces electromagnetic radiation.

In physics, Planck's law describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature $T$ , when there is no net flow of matter or energy between the body and its environment.

Absorbance is defined as "the logarithm of the ratio of incident to transmitted radiant power through a sample ". Alternatively, for samples which scatter light, absorbance may be defined as "the negative logarithm of one minus absorptance, as measured on a uniform sample". The term is used in many technical areas to quantify the results of an experimental measurement. While the term has its origin in quantifying the absorption of light, it is often entangled with quantification of light which is “lost” to a detector system through other mechanisms. What these uses of the term tend to have in common is that they refer to a logarithm of the ratio of a quantity of light incident on a sample or material to that which is detected after the light has interacted with the sample.

In optical physics, transmittance of the surface of a material is its effectiveness in transmitting radiant energy. It is the fraction of incident electromagnetic power that is transmitted through a sample, in contrast to the transmission coefficient, which is the ratio of the transmitted to incident electric field.

In radiometry, radiance is the radiant flux emitted, reflected, transmitted or received by a given surface, per unit solid angle per unit projected area. Radiance is used to characterize diffuse emission and reflection of electromagnetic radiation, and to quantify emission of neutrinos and other particles. The SI unit of radiance is the watt per steradian per square metre. It is a directional quantity: the radiance of a surface depends on the direction from which it is being observed.

In radiometry, irradiance is the radiant flux received by a surface per unit area. The SI unit of irradiance is the watt per square metre (W⋅m⁻²). The CGS unit erg per square centimetre per second (erg⋅cm⁻²⋅s⁻¹) is often used in astronomy. Irradiance is often called intensity, but this term is avoided in radiometry where such usage leads to confusion with radiant intensity. In astrophysics, irradiance is called radiant flux.

The emissivity of the surface of a material is its effectiveness in emitting energy as thermal radiation. Thermal radiation is electromagnetic radiation that most commonly includes both visible radiation (light) and infrared radiation, which is not visible to human eyes. A portion of the thermal radiation from very hot objects is easily visible to the eye.

In radiometry, radiant intensity is the radiant flux emitted, reflected, transmitted or received, per unit solid angle, and spectral intensity is the radiant intensity per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. These are directional quantities. The SI unit of radiant intensity is the watt per steradian, while that of spectral intensity in frequency is the watt per steradian per hertz and that of spectral intensity in wavelength is the watt per steradian per metre —commonly the watt per steradian per nanometre. Radiant intensity is distinct from irradiance and radiant exitance, which are often called intensity in branches of physics other than radiometry. In radio-frequency engineering, radiant intensity is sometimes called radiation intensity.

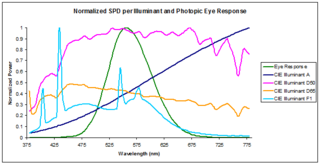
In radiometry, photometry, and color science, a spectral power distribution (SPD) measurement describes the power per unit area per unit wavelength of an illumination. More generally, the term spectral power distribution can refer to the concentration, as a function of wavelength, of any radiometric or photometric quantity.

In radiometry, radiant flux or radiant power is the radiant energy emitted, reflected, transmitted, or received per unit time, and spectral flux or spectral power is the radiant flux per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. The SI unit of radiant flux is the watt (W), one joule per second, while that of spectral flux in frequency is the watt per hertz and that of spectral flux in wavelength is the watt per metre —commonly the watt per nanometre.

In radiometry, radiant exitance or radiant emittance is the radiant flux emitted by a surface per unit area, whereas spectral exitance or spectral emittance is the radiant exitance of a surface per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. This is the emitted component of radiosity. The SI unit of radiant exitance is the watt per square metre, while that of spectral exitance in frequency is the watt per square metre per hertz (W·m⁻²·Hz⁻¹) and that of spectral exitance in wavelength is the watt per square metre per metre (W·m⁻³)—commonly the watt per square metre per nanometre. The CGS unit erg per square centimeter per second is often used in astronomy. Radiant exitance is often called "intensity" in branches of physics other than radiometry, but in radiometry this usage leads to confusion with radiant intensity.

The linear attenuation coefficient, attenuation coefficient, or narrow-beam attenuation coefficient characterizes how easily a volume of material can be penetrated by a beam of light, sound, particles, or other energy or matter. A coefficient value that is large represents a beam becoming 'attenuated' as it passes through a given medium, while a small value represents that the medium had little effect on loss. The SI unit of attenuation coefficient is the reciprocal metre (m⁻¹). Extinction coefficient is another term for this quantity, often used in meteorology and climatology. Most commonly, the quantity measures the exponential decay of intensity, that is, the value of downward e-folding distance of the original intensity as the energy of the intensity passes through a unit thickness of material, so that an attenuation coefficient of 1 m⁻¹ means that after passing through 1 metre, the radiation will be reduced by a factor of e, and for material with a coefficient of 2 m⁻¹, it will be reduced twice by e, or e². Other measures may use a different factor than e, such as the decadic attenuation coefficient below. The broad-beam attenuation coefficient counts forward-scattered radiation as transmitted rather than attenuated, and is more applicable to radiation shielding. The mass attenuation coefficient is the attenuation coefficient normalized by the density of the material.

In the study of heat transfer, absorptance of the surface of a material is its effectiveness in absorbing radiant energy. It is the ratio of the absorbed to the incident radiant power.

In radiometry, radiant exposure or fluence is the radiant energy received by a surface per unit area, or equivalently the irradiance of a surface, integrated over time of irradiation, and spectral exposure is the radiant exposure per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. The SI unit of radiant exposure is the joule per square metre, while that of spectral exposure in frequency is the joule per square metre per hertz and that of spectral exposure in wavelength is the joule per square metre per metre —commonly the joule per square metre per nanometre.

In radiometry, radiant energy density is the radiant energy per unit volume. The SI unit of radiant energy density is the joule per cubic metre (J/m³).

References

↑ FAIRsharing Team (2015). "Radiosity". Quantities, Units, Dimensions and dataTypes. doi:10.25504/FAIRsharing.d3pqw7 . Retrieved 25 February 2021.
↑ Gan, Guohui (September 1994). "Numerical Method for a Full Assessment of Indoor Thermal Comfort". Indoor Air. 4 (3): 154–168. doi: 10.1111/j.1600-0668.1994.t01-1-00004.x .
1 2 3 ISO 9288:1989 – Thermal insulation — Heat transfer by radiation — Physical quantities and definitions.
1 2 Sparrow, Ephraim. M.; Cess, Robert D. (1978). Radiation heat transfer (3rd ed.). Washington, DC: Hemisphere. ISBN 9780070599109.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[note-suffix-e-5] Standards organizations recommend that radiometric quantities should be denoted with suffix "e" (for "energetic") to avoid confusion with photometric or photon quantities.

[note-alternative-symbol-radiometric-6] 1 2 3 4 5 Alternative symbols sometimes seen: $W$ or $E$ for radiant energy, $P$ or $F$ for radiant flux, $I$ for irradiance, $W$ for radiant exitance.

[note-suffix-nu-7] 1 2 3 4 5 6 7 Spectral quantities given per unit frequency are denoted with suffix " ν " (Greek letter nu, not to be confused with a letter "v", indicating a photometric quantity.)

[note-suffix-lambda-8] 1 2 3 4 5 6 7 Spectral quantities given per unit wavelength are denoted with suffix " λ ".

[note-suffix-omega-9] 1 2 Directional quantities are denoted with suffix "Ω".

[1] FAIRsharing Team (2015). "Radiosity". Quantities, Units, Dimensions and dataTypes. doi:10.25504/FAIRsharing.d3pqw7 . Retrieved 25 February 2021.

[2] Gan, Guohui (September 1994). "Numerical Method for a Full Assessment of Indoor Thermal Comfort". Indoor Air. 4 (3): 154–168. doi: 10.1111/j.1600-0668.1994.t01-1-00004.x .

[ISO_9288-1989-3] 1 2 3 ISO 9288:1989 – Thermal insulation — Heat transfer by radiation — Physical quantities and definitions.

[sparrow-4] 1 2 Sparrow, Ephraim. M.; Cess, Robert D. (1978). Radiation heat transfer (3rd ed.). Washington, DC: Hemisphere. ISBN 9780070599109.

[1]

[2]

[3]

[4]

[nb 1]

[nb 2]

[nb 3]

[nb 4]

[nb 5]

Radiosity
Common symbols	$J_{\mathrm {e} }$
SI unit	W·m⁻²
Other units	erg·cm⁻²·s⁻¹
Dimension	MT⁻³