
In physics, optical depth or optical thickness is the natural logarithm of the ratio of incident to transmitted radiant power through a material. Thus, the larger the optical depth, the smaller the amount of transmitted radiant power through the material. Spectral optical depth or spectral optical thickness is the natural logarithm of the ratio of incident to transmitted spectral radiant power through a material. Optical depth is dimensionless, and in particular is not a length, though it is a monotonically increasing function of optical path length, and approaches zero as the path length approaches zero. The use of the term "optical density" for optical depth is discouraged.
The Eddington luminosity, also referred to as the Eddington limit, is the maximum luminosity a body can achieve when there is balance between the force of radiation acting outward and the gravitational force acting inward. The state of balance is called hydrostatic equilibrium. When a star exceeds the Eddington luminosity, it will initiate a very intense radiation-driven stellar wind from its outer layers. Since most massive stars have luminosities far below the Eddington luminosity, their winds are driven mostly by the less intense line absorption. The Eddington limit is invoked to explain the observed luminosities of accreting black holes such as quasars.

In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 to estimate phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice (heat) as phonons in a box in contrast to the Einstein photoelectron model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low-temperature dependence of the heat capacity of solids, which is proportional to – the Debye T 3 law. Similarly to the Einstein photoelectron model, it recovers the Dulong–Petit law at high temperatures. Due to simplifying assumptions, its accuracy suffers at intermediate temperatures.

In heat transfer, Kirchhoff's law of thermal radiation refers to wavelength-specific radiative emission and absorption by a material body in thermodynamic equilibrium, including radiative exchange equilibrium. It is a special case of Onsager reciprocal relations as a consequence of the time reversibility of microscopic dynamics, also known as microscopic reversibility.
The Einstein–Hilbert action in general relativity is the action that yields the Einstein field equations through the stationary-action principle. With the (− + + +) metric signature, the gravitational part of the action is given as
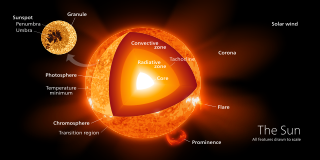
A radiation zone, or radiative region is a layer of a star's interior where energy is primarily transported toward the exterior by means of radiative diffusion and thermal conduction, rather than by convection. Energy travels through the radiation zone in the form of electromagnetic radiation as photons.
In mathematics, the Hankel transform expresses any given function f(r) as the weighted sum of an infinite number of Bessel functions of the first kind Jν(kr). The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r axis. The necessary coefficient Fν of each Bessel function in the sum, as a function of the scaling factor k constitutes the transformed function. The Hankel transform is an integral transform and was first developed by the mathematician Hermann Hankel. It is also known as the Fourier–Bessel transform. Just as the Fourier transform for an infinite interval is related to the Fourier series over a finite interval, so the Hankel transform over an infinite interval is related to the Fourier–Bessel series over a finite interval.

In atomic, molecular, and optical physics, the Einstein coefficients are quantities describing the probability of absorption or emission of a photon by an atom or molecule. The Einstein A coefficients are related to the rate of spontaneous emission of light, and the Einstein B coefficients are related to the absorption and stimulated emission of light. Throughout this article, "light" refers to any electromagnetic radiation, not necessarily in the visible spectrum.
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission, and scattering processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in a wide variety of subjects including optics, astrophysics, atmospheric science, and remote sensing. Analytic solutions to the radiative transfer equation (RTE) exist for simple cases but for more realistic media, with complex multiple scattering effects, numerical methods are required. The present article is largely focused on the condition of radiative equilibrium.
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.
The source function is a characteristic of a stellar atmosphere, and in the case of no scattering of photons, describes the ratio of the emission coefficient to the absorption coefficient. It is a measure of how photons in a light beam are removed and replaced by new photons by the material it passes through. Its units in the cgs-system are erg s−1 cm−2 sr−1 Hz−1 and in SI are W m−2 sr−1 Hz−1. The source function can be written
The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members often asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.
The linear attenuation coefficient, attenuation coefficient, or narrow-beam attenuation coefficient characterizes how easily a volume of material can be penetrated by a beam of light, sound, particles, or other energy or matter. A coefficient value that is large represents a beam becoming 'attenuated' as it passes through a given medium, while a small value represents that the medium had little effect on loss. The (derived) SI unit of attenuation coefficient is the reciprocal metre (m−1). Extinction coefficient is another term for this quantity, often used in meteorology and climatology. Most commonly, the quantity measures the exponential decay of intensity, that is, the value of downward e-folding distance of the original intensity as the energy of the intensity passes through a unit thickness of material, so that an attenuation coefficient of 1 m−1 means that after passing through 1 metre, the radiation will be reduced by a factor of e, and for material with a coefficient of 2 m−1, it will be reduced twice by e, or e2. Other measures may use a different factor than e, such as the decadic attenuation coefficient below. The broad-beam attenuation coefficient counts forward-scattered radiation as transmitted rather than attenuated, and is more applicable to radiation shielding. The mass attenuation coefficient is the attenuation coefficient normalized by the density of the material.
Acoustic streaming is a steady flow in a fluid driven by the absorption of high amplitude acoustic oscillations. This phenomenon can be observed near sound emitters, or in the standing waves within a Kundt's tube. Acoustic streaming was explained first by Lord Rayleigh in 1884. It is the less-known opposite of sound generation by a flow.
f(R) is a type of modified gravity theory which generalizes Einstein's general relativity. f(R) gravity is actually a family of theories, each one defined by a different function, f, of the Ricci scalar, R. The simplest case is just the function being equal to the scalar; this is general relativity. As a consequence of introducing an arbitrary function, there may be freedom to explain the accelerated expansion and structure formation of the Universe without adding unknown forms of dark energy or dark matter. Some functional forms may be inspired by corrections arising from a quantum theory of gravity. f(R) gravity was first proposed in 1970 by Hans Adolph Buchdahl. It has become an active field of research following work by Starobinsky on cosmic inflation. A wide range of phenomena can be produced from this theory by adopting different functions; however, many functional forms can now be ruled out on observational grounds, or because of pathological theoretical problems.
Acoustic radiation force (ARF) is a physical phenomenon resulting from the interaction of an acoustic wave with an obstacle placed along its path. Generally, the force exerted on the obstacle is evaluated by integrating the acoustic radiation pressure over its time-varying surface.
The grey atmosphere is a useful set of approximations made for radiative transfer applications in studies of stellar atmospheres based on the simplified notion that the absorption coefficient of matter within a star's atmosphere is constant—that is, unchanging—for all frequencies of the star's incident radiation.
Kramers' opacity law describes the opacity of a medium in terms of the ambient density and temperature, assuming that the opacity is dominated by bound-free absorption or free-free absorption. It is often used to model radiative transfer, particularly in stellar atmospheres. The relation is named after the Dutch physicist Hendrik Kramers, who first derived the form in 1923.
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product is a product distribution.

In fluid dynamics, the Falkner–Skan boundary layer describes the steady two-dimensional laminar boundary layer that forms on a wedge, i.e. flows in which the plate is not parallel to the flow. It is also representative of flow on a flat plate with an imposed pressure gradient along the plate length, a situation often encountered in wind tunnel flow. It is a generalization of the flat plate Blasius boundary layer in which the pressure gradient along the plate is zero.

























