In combinatorics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colours) of a sufficiently large complete graph. To demonstrate the theorem for two colours (say, blue and red), let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices. (Here R(r, s) signifies an integer that depends on both r and s.)

Ronald Lewis Graham was an American mathematician credited by the American Mathematical Society as "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years". He was president of both the American Mathematical Society and the Mathematical Association of America, and his honors included the Leroy P. Steele Prize for lifetime achievement and election to the National Academy of Sciences.

Fan-Rong King Chung Graham, known professionally as Fan Chung, is a Taiwanese-born American mathematician who works mainly in the areas of spectral graph theory, extremal graph theory and random graphs, in particular in generalizing the Erdős–Rényi model for graphs with general degree distribution.
Ralph Jasper Faudree was a mathematician, a professor of mathematics and the former provost of the University of Memphis.
András Gyárfás is a Hungarian mathematician who specializes in the study of graph theory. He is famous for two conjectures:

Endre Szemerédi is a Hungarian-American mathematician and computer scientist, working in the field of combinatorics and theoretical computer science. He has been the State of New Jersey Professor of computer science at Rutgers University since 1986. He also holds a professor emeritus status at the Alfréd Rényi Institute of Mathematics of the Hungarian Academy of Sciences.

László Lovász is a Hungarian mathematician and professor emeritus at Eötvös Loránd University, best known for his work in combinatorics, for which he was awarded the 2021 Abel Prize jointly with Avi Wigderson. He was the president of the International Mathematical Union from 2007 to 2010 and the president of the Hungarian Academy of Sciences from 2014 to 2020.

Frank Harary was an American mathematician, who specialized in graph theory. He was widely recognized as one of the "fathers" of modern graph theory. Harary was a master of clear exposition and, together with his many doctoral students, he standardized the terminology of graphs. He broadened the reach of this field to include physics, psychology, sociology, and even anthropology. Gifted with a keen sense of humor, Harary challenged and entertained audiences at all levels of mathematical sophistication. A particular trick he employed was to turn theorems into games—for instance, students would try to add red edges to a graph on six vertices in order to create a red triangle, while another group of students tried to add edges to create a blue triangle. Because of the theorem on friends and strangers, one team or the other would have to win.
In mathematics, the Burr–Erdős conjecture was a problem concerning the Ramsey number of sparse graphs. The conjecture is named after Stefan Burr and Paul Erdős, and is one of many conjectures named after Erdős; it states that the Ramsey number of graphs in any sparse family of graphs should grow linearly in the number of vertices of the graph.

Joel Spencer is an American mathematician. He is a combinatorialist who has worked on probabilistic methods in combinatorics and on Ramsey theory. He received his doctorate from Harvard University in 1970, under the supervision of Andrew Gleason. He is currently a professor at the Courant Institute of Mathematical Sciences of New York University. Spencer's work was heavily influenced by Paul Erdős, with whom he coauthored many papers.

Václav (Vašek) Chvátal is a Professor Emeritus in the Department of Computer Science and Software Engineering at Concordia University in Montreal, Quebec, Canada, and a visiting professor at Charles University in Prague. He has published extensively on topics in graph theory, combinatorics, and combinatorial optimization.
In mathematical logic, monadic second-order logic (MSO) is the fragment of second-order logic where the second-order quantification is limited to quantification over sets. It is particularly important in the logic of graphs, because of Courcelle's theorem, which provides algorithms for evaluating monadic second-order formulas over graphs of bounded treewidth. It is also of fundamental importance in automata theory, where the Büchi–Elgot–Trakhtenbrot theorem gives a logical characterization of the regular languages.
In mathematics and social science, a collaboration graph is a graph modeling some social network where the vertices represent participants of that network and where two distinct participants are joined by an edge whenever there is a collaborative relationship between them of a particular kind. Collaboration graphs are used to measure the closeness of collaborative relationships between the participants of the network.
In abstract algebra, the group isomorphism problem is the decision problem of determining whether two given finite group presentations refer to isomorphic groups.
János Pach is a mathematician and computer scientist working in the fields of combinatorics and discrete and computational geometry.
András Hajnal was a professor of mathematics at Rutgers University and a member of the Hungarian Academy of Sciences known for his work in set theory and combinatorics.
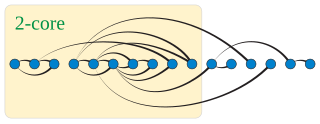
In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has at least one vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.
Jon Hal Folkman was an American mathematician, a student of John Milnor, and a researcher at the RAND Corporation.
Michael S. Jacobson is a mathematician, and Professor of Mathematical & Statistical Sciences in the Department of Mathematical & Statistical Science at the University of Colorado Denver. He served as Chair from 2003 to 2012 and was on loan serving as a program director in EHR/DUE at the National Science Foundation.