| Stemphylium sarciniforme | |
|---|---|
 | |
| Leaf damage from Stemphylium sarciniforme | |
Scientific classification  | |
| Kingdom: | Fungi |
| Division: | Ascomycota |
| Class: | Dothideomycetes |
| Order: | Pleosporales |
| Family: | Pleosporaceae |
| Genus: | Stemphylium |
| Species: | S. sarciniforme |
| Binomial name | |
| Stemphylium sarciniforme (Cavara) Wiltshire [as 'sarcinaeforme'], (1938) | |
| Synonyms | |
Macrosporium sarciniformeCavara [as 'sarcinaeforme'], (1890) | |
Stemphylium sarciniforme is a plant pathogen infecting lentil, red clover and chickpea.
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities. The orientation of an object's acceleration is given by the orientation of the net force acting on that object. The magnitude of an object's acceleration, as described by Newton's Second Law, is the combined effect of two causes:
In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes. The same amount of work is done by the body when decelerating from its current speed to a state of rest. Formally, a kinetic energy is any term in a system's Lagrangian which includes a derivative with respect to time.
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz.
In Newtonian mechanics, linear momentum, translational momentum, or simply momentum is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If m is an object's mass and v is its velocity, then the object's momentum p is :
In physics, power is the amount of energy transferred or converted per unit time. In the International System of Units, the unit of power is the watt, equal to one joule per second. In older works, power is sometimes called activity. Power is a scalar quantity.
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Objects that tensors may map between include vectors and scalars, and even other tensors. There are many types of tensors, including scalars and vectors, dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system.
In electrical engineering, impedance is the opposition to alternating current presented by the combined effect of resistance and reactance in a circuit.
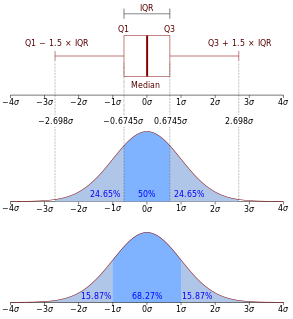
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would be close to that sample. In other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample.
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form:
In physics, work is the energy transferred to or from an object via the application of force along a displacement. In its simplest form, it is often represented as the product of force and displacement. A force is said to do positive work if it has a component in the direction of the displacement of the point of application. A force does negative work if it has a component opposite to the direction of the displacement at the point of application of the force.
In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions.
In biochemistry, Michaelis–Menten kinetics is one of the best-known models of enzyme kinetics. It is named after German biochemist Leonor Michaelis and Canadian physician Maud Menten. The model takes the form of an equation describing the rate of enzymatic reactions, by relating reaction rate to , the concentration of a substrate S. Its formula is given by
In physics and relativity, time dilation is the difference in the elapsed time as measured by two clocks. It is either due to a relative velocity between them or to a difference in gravitational potential between their locations. When unspecified, "time dilation" usually refers to the effect due to velocity.
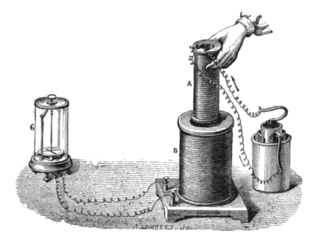
Faraday's law of induction is a basic law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (emf)—a phenomenon known as electromagnetic induction. It is the fundamental operating principle of transformers, inductors, and many types of electrical motors, generators and solenoids.
In fluid dynamics, drag is a force acting opposite to the relative motion of any object moving with respect to a surrounding fluid. This can exist between two fluid layers or between a fluid and a solid surface. Unlike other resistive forces, such as dry friction, which are nearly independent of velocity, the drag force depends on velocity.
In linear algebra, an eigenvector or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by , is the factor by which the eigenvector is scaled.
A capacitor is a device that stores electrical energy in an electric field. It is a passive electronic component with two terminals.
Velocity is the directional speed of a object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time. Velocity is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of bodies.
In mathematics, Hilbert spaces allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. A Hilbert space is a vector space equipped with an inner product which defines a distance function for which it is a complete metric space. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces.
 | This Pleosporales-related article is a stub. You can help Wikipedia by expanding it. |