In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two pyramids together base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usually coplanar and a bipyramid is usually symmetric, meaning the two pyramids are mirror images across their common base plane. When each apex of the bipyramid is on a line perpendicular to the base and passing through its center, it is a right bipyramid; otherwise it is oblique. When the base is a regular polygon, the bipyramid is also called regular.
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a strictly convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two solids with such a property: the first solids are the pyramids, cupolas. and a rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. These solids are named after mathematicians Norman Johnson and Victor Zalgaller.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square, it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In geometry, the triangular bipyramid is the hexahedron with six triangular faces, constructed by attaching two tetrahedra face-to-face. The same shape is also called the triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of triangular bipyramid are equilateral. It is an example of a deltahedron and of a Johnson solid.
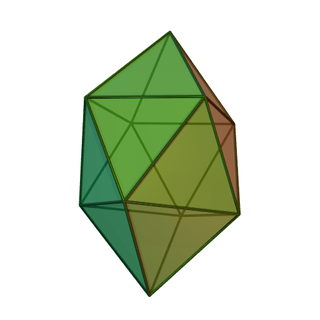
In geometry, the gyroelongated square bipyramid is a polyhedron with 16 triangular faces. it can be constructed from a square antiprism by attaching two equilateral square pyramids to each of its square faces. The same shape is also called hexakaidecadeltahedron, heccaidecadeltahedron, or tetrakis square antiprism; these last names mean a polyhedron with 16 triangular faces. It is an example of deltahedron, and of a Johnson solid.

In geometry, the pentagonal bipyramid is a polyhedron with 10 triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an example of deltahedra, and of Johnson solid.

In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape also has alternative names called Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron; these names mean the 12-sided polyhedron.
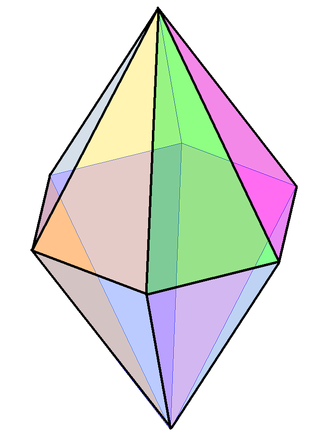
A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.

In geometry, a triangular prism or trigonal prism is a prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a right triangular prism. A right triangular prism may be both semiregular and uniform.

In geometry, a trigonal trapezohedron is a polyhedron with six congruent quadrilateral faces, which may be scalene or rhomboid. The variety with rhombus-shaped faces faces is a rhombohedron. An alternative name for the same shape is the trigonal deltohedron.

The hexagonal bifrustum or truncated hexagonal bipyramid is the fourth in an infinite series of bifrustum polyhedra. It has 12 trapezoid and 2 hexagonal faces. This polyhedron can be constructed by taking a hexagonal dipyramid and truncating the polar axis vertices, making it into two end-to-end frustums.

In geometry, an n-agonal bifrustum is a polyhedron composed of three parallel planes of n-agons, with the middle plane largest and usually the top and bottom congruent.
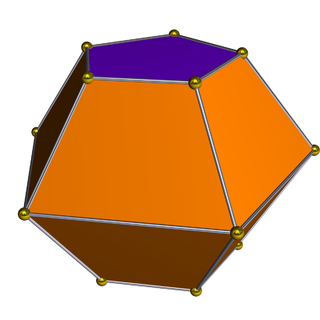
In geometry, the pentagonal bifrustum or truncated pentagonal bipyramid is the third in an infinite series of bifrustum polyhedra. It has 10 trapezoidal and 2 pentagonal faces.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.

A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.

A geodesic polyhedron is a convex polyhedron made from triangles. They usually have icosahedral symmetry, such that they have 6 triangles at a vertex, except 12 vertices which have 5 triangles. They are the dual of corresponding Goldberg polyhedra, of which all but the smallest one have mostly hexagonal faces.



















